Cho tứ diện S.ABC có SA vuông góc với mặt phẳng (ABC), SA=AB=3cm, BC=5cm và diện

Trả lời

Gắn trục t$\text{C}\left(0;4;0\right),\text{ S}\left(0;0;3\right)$ọa độ Ox, Oy, Oz như hình vẽ.

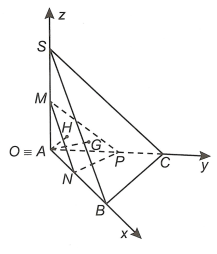
Vì tam giác SAC vuông tại A

$\Rightarrow AC=\frac{2S_{\Delta SAC}}{SA}=4cm$

Vì $A{C}^2+A{B}^2=B{C}^2$  nên tam giác ABC vuông tại A.

Chọn hệ trục Oxyz như hình vẽ.

Ta có $A\left(0;0;0\right),\text{ B}\left(3;0;0\right)$ ,

Vì G là trọng tâm của tứ diện S.ABC nên ta có:

$\left\{\begin{array}{l}{x}_G=\frac{x_S+x_A+x_B+x_C}{4}=\frac{3}{4}\\ y_G=\frac{y_S+y_A+y_B+y_C}{4}=1\\ z_G=\frac{z_S+z_A+z_B+z_C}{4}=\frac{3}{4}\end{array}\right.\Rightarrow G\left(\frac{3}{4};1;\frac{3}{4}\right)$

Gọi H là hình chiếu của điểm A lên mặt phẳng $\left(\alpha \right)$ . Theo tính chất của tam diện vuông ta có: $T=\frac{1}{A{M}^2}+\frac{1}{A{N}^2}+\frac{1}{A{P}^2}=\frac{1}{A{H}^2}$ .

Mà $AH\le AG\Rightarrow T=\frac{1}{A{M}^2}+\frac{1}{A{N}^2}+\frac{1}{A{P}^2}=\frac{1}{A{H}^2}\ge \frac{1}{A{G}^2}\Rightarrow T\ge \frac{8}{17}$ .

Dấu “=” xảy ra khi $H\equiv G$  tức mặt phẳng $\left(\alpha \right)$  đi qua điểm G và vuông góc với đường thẳng OG.

Vậy giá trị nhỏ nhất của T bằng $\frac{8}{17}$ .

Chọn A.