Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA=2a và vuông

Trả lời

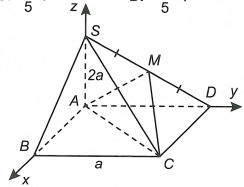
Để thuận tiện trong việc tính toán ta chọn $a=1$ .

Trong không gian, gắn hệ trục tọa độ Oxyz như hình vẽ sao cho gốc O trùng với điểm A, tia Ox trùng với tia AB, tia Oy trùng với tia AD, tia Oz trùng với tia AS.

Khi đó $A\left(0;0;0\right),\text{ B}\left(1;0;0\right),\text{ C}\left(1;1;0\right),\text{ S}\left(0;0;2\right),\text{ D}\left(0;1;0\right)$ .

Vì M là trung điểm SD nên tọa độ M là $M\left(0;\frac{1}{2};1\right)$ .

Ta có $\left\{\begin{array}{l}\overrightarrow{SB}=\left(1;0;-2\right)\\ \overrightarrow{BC}=\left(0;1;0\right)\end{array}\right.\Rightarrow {\overrightarrow{n}}_{\left(SBC\right)}=\left[\overrightarrow{SB};\overrightarrow{BC}\right]=\left(2;0;1\right)$ .

$\left\{\begin{array}{l}\overrightarrow{AM}=\left(0;\frac{1}{2};1\right)\\ \overrightarrow{AC}=\left(1;1;0\right)\end{array}\right.\Rightarrow {\overrightarrow{n}}_{\left(AMC\right)}=\left[\overrightarrow{AM};\overrightarrow{AC}\right]=\left(-1;1;\frac{-1}{2}\right)$

Góc $\alpha$  là góc giữa hai mặt phẳng $\left(AMC\right)$  và $\left(SBC\right)$ .

Suy ra $\cos \alpha =\left|\cos \left({\overrightarrow{n}}_{\left(SBC\right)};{\overrightarrow{n}}_{\left(AMC\right)}\right)\right|=\frac{\left|{\overrightarrow{n}}_{\left(SBC\right)}.{\overrightarrow{n}}_{\left(AMC\right)}\right|}{\left|{\overrightarrow{n}}_{\left(SBC\right)}\right|.\left|{\overrightarrow{n}}_{\left(AMC\right)}\right|}=\frac{\sqrt{5}}{3}$ .

Mặt khác, $1+{\tan }^2\alpha =\frac{1}{{\cos }^2\alpha }\Rightarrow \tan \alpha =\sqrt{\frac{1}{{\cos }^2\alpha }-1}$ .

Vậy $\tan \alpha =\sqrt{\frac{1}{{\left(\frac{\sqrt{5}}{3}\right)}^2}-1}=\frac{2\sqrt{5}}{5}$ .

Chọn D.