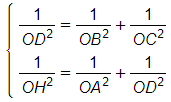Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau. Gọi H là hình chiếu của điểm O trên mặt phẳng (ABC)
339
07/12/2023
Bài 1 trang 76 SBT Toán 11 Tập 2: Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau. Gọi H là hình chiếu của điểm O trên mặt phẳng (ABC). Chứng minh rằng:
a) BC ⊥ (OAH).
b) H là trực tâm của ∆ABC.
c) 1OH2=1OA2+1OB2+1OC2 .
Trả lời
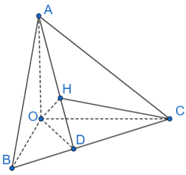
a)Ta có: 
⇒OA⊥(OBC)⇒OA⊥BC.(1)
OH⊥BC (OH⊥(ABC)).(2)
Từ (1) và (2) ⇒ BC ⊥ (OAH).
b)Từ a) ⇒ BC ⊥ AH. (*)
Ta dễ dàng chứng minh được OC ⊥ (OAB) ⇒ OC ⊥ AB. (3)
Lại có: OH ⊥ AB (do OH ⊥ (ABC)) ⇒ OH ⊥ AB. (4)
Từ (3) và (4) ⇒ AB ⊥ (OHC) hay AB ⊥ HC. (**)
Từ (*) và (**) ⇒ H là trực tâm của tam giác ABC.
c)Dễ thấy OD, OH là các đường cao của tam giác OBC và OAD.
Áp dụng hệ thức lượng trong tam giác vuông, ta có:
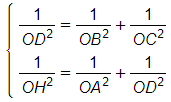
Do đó 1OH2=1OA2+1OB2+1OC2.
Xem thêm các bài giải SBT Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác: