Cho tứ diện đều ABCD có độ dài các cạnh bằng a. Gọi M là trung điểm của CD, kẻ AH vuông góc với BM tại H

Bài 7.19 trang 34 SBT Toán 11 Tập 2: Cho tứ diện đều ABCD có độ dài các cạnh bằng a. Gọi M là trung điểm của CD, kẻ AH vuông góc với BM tại H.

a) Chứng minh rằng AH $\perp$ (BCD).

b) Tính côsin của góc giữa mặt phẳng (BCD) và mặt phẳng (ACD).

Trả lời

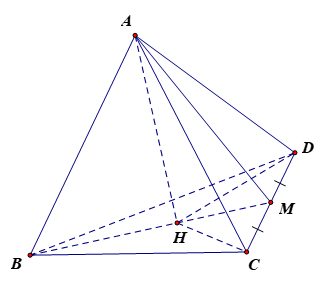
a) Vì M là trung điểm của CD nên BM là trung tuyến.

Vì BCD là tam giác đều nên CD $\perp$ BM.

Tương tự CD $\perp$ AM nên CD $\perp$ (ABM), suy ra CD ^ AH.

Mà AH $\perp$ BM nên AH $\perp$ (BCD).

b) Vì AM $\perp$ CD, BM $\perp$ CD nên góc giữa hai mặt phẳng (BCD) và mặt phẳng (ACD) bằng góc giữa hai đường thẳng AM và BM, mà (AB,BM) = $\widehat{AMB}$.

Tam giác BCD đều có BM là đường cao đồng thời là trung tuyến, ta chứng minh được H là trọng tâm tam giác BCD nên BM = $\frac{a\sqrt{3}}{2}$ và HM = $\frac{1}{3}$BM = $\frac{a\sqrt{3}}{6}$.

Tam giác ADC đều có AM là đường cao đồng thời là trung tuyến nên AM = $\frac{a\sqrt{3}}{2}$ .

Xét tam giác AHM vuông tại H nên cos$\widehat{AMB}$ = cos$\widehat{AMH}=\frac{HM}{AM}=\frac{1}{3}$.

Vậy côsin của góc giữa mặt phẳng (BCD) và mặt phẳng (ACD) bằng $\frac{1}{3}$ .

Xem thêm các bài giải SBT Toán lớp 11 Kết nối tri thức hay, chi tiết khác:

Bài 23: Đường thẳng vuông góc với mặt phẳng

Bài 24: Phép chiếu vuông góc. Góc giữa đường thẳng và mặt phẳng

Bài 25: Hai mặt phẳng vuông góc

Bài 26: Khoảng cách

Bài 27: Thể tích

Bài tập cuối chương 7