Câu hỏi:
03/04/2024 29
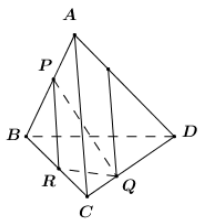
Cho tứ diện ABCD và ba điểm P, Q, R lần lượt nằm trên các cạnh AB, CD, BC (không trùng với các đỉnh của tứ diện ABCD) sao cho \[PR\parallel AC\]. Khi đó giao tuyến của hai mặt phẳng \[\left( {PQR} \right)\] và \[\left( {ACD} \right)\] song song với đường thẳng nào trong các đường thẳng sau?
A. BD
B. CD
C. CB
D. AC
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án D
Phương pháp:
Giao tuyến của hai mặt phẳng chứa hai đường thẳng song song là đường thẳng đi qua 1 điểm chung của hai mặt phẳng và song song với hai đường thẳng đó.
Cách giải:
Ta có \[\left\{ \begin{array}{l}Q \in \left( {PQR} \right)\\Q \in CD \subset \left( {ACD} \right) \Rightarrow Q \in \left( {ACD} \right)\end{array} \right. \Rightarrow Q \in \left( {PQR} \right) \cap \left( {ACD} \right)\]
\[\left\{ \begin{array}{l}\left( {PQR} \right) \supset PR\\\left( {ACD} \right) \supset AC\\PR\parallel AC\end{array} \right. \Rightarrow \] Giao tuyến của hai mặt phẳng \[\left( {PQR} \right)\] và \[\left( {ACD} \right)\]
là đường thẳng đi qua Q và song song với AC, PR.
Đáp án D
Phương pháp:
Giao tuyến của hai mặt phẳng chứa hai đường thẳng song song là đường thẳng đi qua 1 điểm chung của hai mặt phẳng và song song với hai đường thẳng đó.
Cách giải:
Ta có \[\left\{ \begin{array}{l}Q \in \left( {PQR} \right)\\Q \in CD \subset \left( {ACD} \right) \Rightarrow Q \in \left( {ACD} \right)\end{array} \right. \Rightarrow Q \in \left( {PQR} \right) \cap \left( {ACD} \right)\]
\[\left\{ \begin{array}{l}\left( {PQR} \right) \supset PR\\\left( {ACD} \right) \supset AC\\PR\parallel AC\end{array} \right. \Rightarrow \] Giao tuyến của hai mặt phẳng \[\left( {PQR} \right)\] và \[\left( {ACD} \right)\]
là đường thẳng đi qua Q và song song với AC, PR.

CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Chọn ngẫu nhiên một số nguyên dương nhỏ hơn 9, xác suất để số được chọn là số nguyên tố bằng:
Câu 2:
Số các số tự nhiên có 5 chữ số khác nhau lập được từ các chữ số 1, 2, 3, 4, 5, 6, 7, 8 là:
Câu 3:
b) Nếu các câu hỏi trong đề thi được chọn ngẫu nhiên. Tính xác suất để trong đề thi có đủ ba loại câu hỏi sao cho số câu dễ và câu trung bình bằng nhau.
b) Nếu các câu hỏi trong đề thi được chọn ngẫu nhiên. Tính xác suất để trong đề thi có đủ ba loại câu hỏi sao cho số câu dễ và câu trung bình bằng nhau.
Câu 4:
Hệ số của \[{x^3}\] trong khai triển nhị thức Niu – Tơn của \[{\left( {2 + x} \right)^{10}}\] là:
Câu 6:
Trong ngân hàng đề có 6 câu hỏi dễ, 5 câu hỏi trung bình và 3 câu hỏi khó. Một đề thi gồm có 6 câu hỏi được chọn từ các câu trong ngân hàng đề đã cho.
a) Hỏi có tất cả bao nhiêu đề thi khác nhau nếu trong đề có 3 câu dễ, 2 câu trung bình và 1 câu khó.
Trong ngân hàng đề có 6 câu hỏi dễ, 5 câu hỏi trung bình và 3 câu hỏi khó. Một đề thi gồm có 6 câu hỏi được chọn từ các câu trong ngân hàng đề đã cho.
a) Hỏi có tất cả bao nhiêu đề thi khác nhau nếu trong đề có 3 câu dễ, 2 câu trung bình và 1 câu khó.
Câu 7:
Cho 5 điểm A, B, C, D, E trong đó không có 4 điểm nào đồng phẳng. Hỏi có bao nhiêu mặt phẳng tạo bởi 3 trong 5 điểm đã cho?
Câu 8:
Trong mặt phẳng tọa độ Oxy, cho đường tròn \[\left( C \right):{\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = 4\], phép vị tự tâm O tỷ số \[k = 2\] biến đường tròn \[\left( C \right)\] thành đường tròn có phương trình là:
Câu 9:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, M là trung điểm SA, điểm N thuộc đoạn SD sao cho \[NS = 2ND,I\] là giao điểm của MN và AD.
a) Xác định giao tuyến của mặt phẳng \[\left( {BMN} \right)\] với mặt phẳng \[\left( {ABCD} \right)\].
b) Gọi J là giao điểm của CD với BI. Xác định giao tuyến của mặt phẳng \[\left( {BMN} \right)\] với mặt phẳng \[\left( {SCD} \right)\], từ đó suy ra thiết diện của hình chóp với mặt phẳng \[\left( {BMN} \right)\].
c) Gọi K là giao điểm của BI với AC. Chứng minh \[BM\parallel KN\].
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, M là trung điểm SA, điểm N thuộc đoạn SD sao cho \[NS = 2ND,I\] là giao điểm của MN và AD.
a) Xác định giao tuyến của mặt phẳng \[\left( {BMN} \right)\] với mặt phẳng \[\left( {ABCD} \right)\].
b) Gọi J là giao điểm của CD với BI. Xác định giao tuyến của mặt phẳng \[\left( {BMN} \right)\] với mặt phẳng \[\left( {SCD} \right)\], từ đó suy ra thiết diện của hình chóp với mặt phẳng \[\left( {BMN} \right)\].
c) Gọi K là giao điểm của BI với AC. Chứng minh \[BM\parallel KN\].


