Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD và (P) là mặt phẳng
284
09/09/2023
Bài 4.44 trang 71 SBT Toán 11 Tập 1: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD và (P) là mặt phẳng cố định không song song với MN. Gọi A’, B’, C’, D’, M’, N’ lần lượt là hình chiếu của A, B, C, D, M, N qua phép chiếu lên mặt phẳng (P) theo phương MN.
a) Chứng minh rằng hai điểm M’ và N’ trùng nhau.
b) Chứng minh rằng bốn điểm A’, B’, C’, D’ là bốn đỉnh của một hình bình hành.
Trả lời
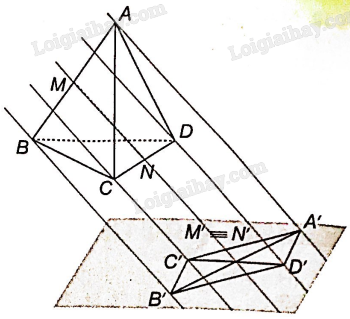
a) Vì đường thẳng MN là phương chiếu nên M’ của M trùng với hình chiếu N’ của N.
b) Vì M là trung điểm của AB nên theo tính chất của phép chiếu song song suy ra M’ là trung điểm của A’B’.
Vì N là trung điểm của CD nên theo tính chất của phép chiếu song song suy ra N’ là trung điểm của C’D’.
Vì M’ trùng N’ nên tứ giác tạo bởi bốn điểm A’, B’, C’, D’ có các đường chéo đi qua trung điểm của mỗi đường, suy ra tứ giác đó là hình bình hành.
Xem thêm các bài giải SBT Toán lớp 11 Kết nối tri thức hay, chi tiết khác:
Bài 12: Đường thẳng và mặt phẳng song song
Bài 13: Hai mặt phẳng song song
Bài 14: Phép chiếu song song
Bài tập cuối chương 4
Bài 15: Giới hạn của dãy số
Bài 16: Giới hạn của hàm số

