Câu hỏi:
19/12/2023 276
Cho tam giác đều ABC có độ dài cạnh bằng a. Trên các cạnh BC, CA, AB lần lượt lấy các điểm N, M, P sao cho \(BN = \frac{a}{3},CM = \frac{{2a}}{3},AP = x\left( {0 < x < a} \right)\). Tìm giá trị của x theo a để đường thẳng AN vuông góc với đường thẳng PM.
Cho tam giác đều ABC có độ dài cạnh bằng a. Trên các cạnh BC, CA, AB lần lượt lấy các điểm N, M, P sao cho \(BN = \frac{a}{3},CM = \frac{{2a}}{3},AP = x\left( {0 < x < a} \right)\). Tìm giá trị của x theo a để đường thẳng AN vuông góc với đường thẳng PM.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
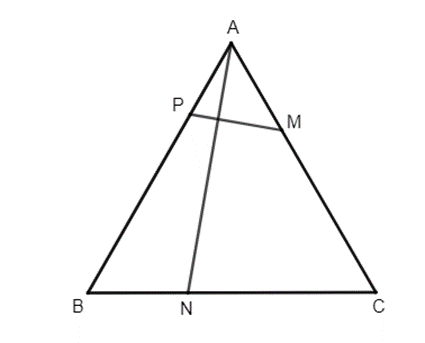
Do BN = \(\frac{a}{3}\) và BC = a nên BN = \(\frac{1}{3}\)BC.
Mà N thuộc cạnh BC nên vectơ \(\overrightarrow {BN} \) và \(\overrightarrow {BC} \) cùng hướng. Do đó, \(\overrightarrow {BN} = \frac{1}{3}\overrightarrow {BC} \).
Ta có \(\overrightarrow {AN} = \overrightarrow {AB} + \overrightarrow {BN} = \overrightarrow {AB} + \frac{1}{3}(\overrightarrow {AC} - \overrightarrow {AB} ) = \frac{2}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} \).
Lại có: CM = \(\frac{{2a}}{3}\), mà AC = a và M thuộc cạnh AC nên AM = \(a - \frac{{2a}}{3} = \frac{a}{3} = \frac{1}{3}AC\).
Suy ra \(\overrightarrow {AM} = \frac{1}{3}\overrightarrow {AC} \).
Và AP = x (0 < x < a), AB = a, P thuộc cạnh AB nên AP = \(\frac{x}{a}AB\).
Suy ra \(\overrightarrow {AP} = \frac{x}{a}\overrightarrow {AB} \).
Do đó, ta có: \(\overrightarrow {PM} = \overrightarrow {AM} - \overrightarrow {AP} = \frac{1}{3}\overrightarrow {AC} - \frac{x}{a}\overrightarrow {AB} \).
Khi đó, \(AN \bot PM \Leftrightarrow \overrightarrow {AN} \cdot \overrightarrow {PM} = 0\)
\( \Leftrightarrow \left( {\frac{2}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} } \right) \cdot \left( {\frac{1}{3}\overrightarrow {AC} - \frac{x}{a}\overrightarrow {AB} } \right) = 0\)
\( \Leftrightarrow \frac{2}{9}\overrightarrow {AB} \cdot \overrightarrow {AC} - \frac{{2x}}{{3a}}{\overrightarrow {AB} ^2} - \frac{x}{{3a}}\overrightarrow {AB} \cdot \overrightarrow {AC} + \frac{1}{9}{\overrightarrow {AC} ^2} = 0\)
\( \Leftrightarrow \left( {\frac{2}{9} - \frac{x}{{3a}}} \right)\overrightarrow {AB} \cdot \overrightarrow {AC} - \frac{{2x}}{{3a}}.{a^2} + \frac{1}{9}.{a^2} = 0\) (do AB = AC = a)
\( \Leftrightarrow \left( {\frac{2}{9} - \frac{x}{{3a}}} \right) \cdot \left| {\overrightarrow {AB} } \right| \cdot \left| {\overrightarrow {AC} } \right| \cdot cos\left( {\overrightarrow {AB} ,\,\,\overrightarrow {AC} } \right) - \frac{{2xa}}{3} + \frac{{{a^2}}}{9} = 0\)
\( \Leftrightarrow \left( {\frac{2}{9} - \frac{x}{{3a}}} \right) \cdot a \cdot a \cdot cos60^\circ - \frac{{2xa}}{3} + \frac{{{a^2}}}{9} = 0\)
\( \Leftrightarrow \frac{{2a - 3x}}{{9a}} \cdot \frac{{{a^2}}}{2} - \frac{{2xa}}{3} + \frac{{{a^2}}}{9} = 0\)
\( \Leftrightarrow \frac{{\left( {2a - 3x} \right)a}}{{18}} - \frac{{12xa}}{{18}} + \frac{{2{a^2}}}{{18}} = 0\)
\( \Leftrightarrow \frac{{2{a^2} - 3xa - 12xa + 2{a^2}}}{{18}} = 0\)
⇔ 4a2 – 15xa = 0
⇔ a(4a – 15x) = 0
⇔ 4a – 15x = 0 (do a > 0).
⇔ \(x = \frac{{4a}}{{15}}\).
Vậy \(x = \frac{{4a}}{{15}}\) thì đường thẳng AN vuông góc với đường thẳng PM.

Do BN = \(\frac{a}{3}\) và BC = a nên BN = \(\frac{1}{3}\)BC.
Mà N thuộc cạnh BC nên vectơ \(\overrightarrow {BN} \) và \(\overrightarrow {BC} \) cùng hướng. Do đó, \(\overrightarrow {BN} = \frac{1}{3}\overrightarrow {BC} \).
Ta có \(\overrightarrow {AN} = \overrightarrow {AB} + \overrightarrow {BN} = \overrightarrow {AB} + \frac{1}{3}(\overrightarrow {AC} - \overrightarrow {AB} ) = \frac{2}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} \).
Lại có: CM = \(\frac{{2a}}{3}\), mà AC = a và M thuộc cạnh AC nên AM = \(a - \frac{{2a}}{3} = \frac{a}{3} = \frac{1}{3}AC\).
Suy ra \(\overrightarrow {AM} = \frac{1}{3}\overrightarrow {AC} \).
Và AP = x (0 < x < a), AB = a, P thuộc cạnh AB nên AP = \(\frac{x}{a}AB\).
Suy ra \(\overrightarrow {AP} = \frac{x}{a}\overrightarrow {AB} \).
Do đó, ta có: \(\overrightarrow {PM} = \overrightarrow {AM} - \overrightarrow {AP} = \frac{1}{3}\overrightarrow {AC} - \frac{x}{a}\overrightarrow {AB} \).
Khi đó, \(AN \bot PM \Leftrightarrow \overrightarrow {AN} \cdot \overrightarrow {PM} = 0\)
\( \Leftrightarrow \left( {\frac{2}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} } \right) \cdot \left( {\frac{1}{3}\overrightarrow {AC} - \frac{x}{a}\overrightarrow {AB} } \right) = 0\)
\( \Leftrightarrow \frac{2}{9}\overrightarrow {AB} \cdot \overrightarrow {AC} - \frac{{2x}}{{3a}}{\overrightarrow {AB} ^2} - \frac{x}{{3a}}\overrightarrow {AB} \cdot \overrightarrow {AC} + \frac{1}{9}{\overrightarrow {AC} ^2} = 0\)
\( \Leftrightarrow \left( {\frac{2}{9} - \frac{x}{{3a}}} \right)\overrightarrow {AB} \cdot \overrightarrow {AC} - \frac{{2x}}{{3a}}.{a^2} + \frac{1}{9}.{a^2} = 0\) (do AB = AC = a)
\( \Leftrightarrow \left( {\frac{2}{9} - \frac{x}{{3a}}} \right) \cdot \left| {\overrightarrow {AB} } \right| \cdot \left| {\overrightarrow {AC} } \right| \cdot cos\left( {\overrightarrow {AB} ,\,\,\overrightarrow {AC} } \right) - \frac{{2xa}}{3} + \frac{{{a^2}}}{9} = 0\)
\( \Leftrightarrow \left( {\frac{2}{9} - \frac{x}{{3a}}} \right) \cdot a \cdot a \cdot cos60^\circ - \frac{{2xa}}{3} + \frac{{{a^2}}}{9} = 0\)
\( \Leftrightarrow \frac{{2a - 3x}}{{9a}} \cdot \frac{{{a^2}}}{2} - \frac{{2xa}}{3} + \frac{{{a^2}}}{9} = 0\)
\( \Leftrightarrow \frac{{\left( {2a - 3x} \right)a}}{{18}} - \frac{{12xa}}{{18}} + \frac{{2{a^2}}}{{18}} = 0\)
\( \Leftrightarrow \frac{{2{a^2} - 3xa - 12xa + 2{a^2}}}{{18}} = 0\)
⇔ 4a2 – 15xa = 0
⇔ a(4a – 15x) = 0
⇔ 4a – 15x = 0 (do a > 0).
⇔ \(x = \frac{{4a}}{{15}}\).
Vậy \(x = \frac{{4a}}{{15}}\) thì đường thẳng AN vuông góc với đường thẳng PM.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Một cảnh sát giao thông ghi lại tốc độ (đơn vị: km/h) của 25 xe qua trạm như sau:
20
41
41
80
40
52
52
52
60
55
60
60
62
60
55
60
55
90
70
35
40
30
30
80
25
Tìm các số liệu bất thường (nếu có) trong mẫu số liệu trên.
Một cảnh sát giao thông ghi lại tốc độ (đơn vị: km/h) của 25 xe qua trạm như sau:
|
20 |
41 |
41 |
80 |
40 |
52 |
52 |
52 |
60 |
55 |
60 |
60 |
62 |
|
60 |
55 |
60 |
55 |
90 |
70 |
35 |
40 |
30 |
30 |
80 |
25 |
|
Tìm các số liệu bất thường (nếu có) trong mẫu số liệu trên.
Câu 2:
Trong mặt phẳng tọa độ Oxy, cho \(\overrightarrow u = - 2\overrightarrow i + \overrightarrow j \). Tìm tọa độ của vectơ \(\overrightarrow u \).
Trong mặt phẳng tọa độ Oxy, cho \(\overrightarrow u = - 2\overrightarrow i + \overrightarrow j \). Tìm tọa độ của vectơ \(\overrightarrow u \).
Câu 3:
Trong mặt phẳng tọa độ Oxy cho ba điểm A(2; 1), B(1; 10) và điểm C(m; 2m – 17). Tất cả các giá trị của tham số m sao cho AB vuông góc với OC là
Trong mặt phẳng tọa độ Oxy cho ba điểm A(2; 1), B(1; 10) và điểm C(m; 2m – 17). Tất cả các giá trị của tham số m sao cho AB vuông góc với OC là
Câu 5:
Một lực \(\overrightarrow F \) có độ lớn \(60\sqrt 3 \) N tác động vào điểm M làm vật di chuyển theo phương nằm ngang từ M đến điểm N cách M một khoảng 10 m. Biết góc giữa \(\overrightarrow F \) và phương thẳng đứng là 30°. Tính công sinh bởi lực F.
Một lực \(\overrightarrow F \) có độ lớn \(60\sqrt 3 \) N tác động vào điểm M làm vật di chuyển theo phương nằm ngang từ M đến điểm N cách M một khoảng 10 m. Biết góc giữa \(\overrightarrow F \) và phương thẳng đứng là 30°. Tính công sinh bởi lực F.
Câu 6:
Cho hình chữ nhật ABCD có AB = 4 cm, AD = 3 cm. Tính \(\left| {\overrightarrow {BC} + \overrightarrow {BA} } \right|\).
Cho hình chữ nhật ABCD có AB = 4 cm, AD = 3 cm. Tính \(\left| {\overrightarrow {BC} + \overrightarrow {BA} } \right|\).
Câu 7:
Cho G là trọng tâm của tam giác ABC và điểm M bất kỳ. Đẳng thức nào sau đây đúng?
Cho G là trọng tâm của tam giác ABC và điểm M bất kỳ. Đẳng thức nào sau đây đúng?
Câu 9:
Cho hình bình hành ABCD. Gọi M, N lần lượt là hai điểm nằm trên hai cạnh AB và CD sao cho AB = 3AM, CD = 2CN. Biểu diễn vectơ \(\overrightarrow {AN} \) qua các vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \).
Cho hình bình hành ABCD. Gọi M, N lần lượt là hai điểm nằm trên hai cạnh AB và CD sao cho AB = 3AM, CD = 2CN. Biểu diễn vectơ \(\overrightarrow {AN} \) qua các vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \).
Câu 11:
Cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) khác vectơ-không. Khẳng định nào sau đây là đúng?
Cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) khác vectơ-không. Khẳng định nào sau đây là đúng?
Câu 12:
Cho góc α với 0° < α < 180°. Tính giá trị của cosα, biết \(\tan \alpha = - 2\sqrt 2 \) .
Cho góc α với 0° < α < 180°. Tính giá trị của cosα, biết \(\tan \alpha = - 2\sqrt 2 \) .
Câu 13:
Miền nghiệm của bất phương trình 2x – y + 6 ≤ 0 được biểu diễn là miền màu xanh trong hình ảnh nào sau đây ?
Miền nghiệm của bất phương trình 2x – y + 6 ≤ 0 được biểu diễn là miền màu xanh trong hình ảnh nào sau đây ?
Câu 15:
Từ hai vị trí A và B của một tòa nhà, người ta quan sát đỉnh C của ngọn núi. Biết rằng độ cao AB = 70 m, phương nhìn AC tạo với phương nằm ngang góc 30°, phương nhìn BC tạo với phương nằm ngang góc 15°30'. Ngọn núi đó có độ cao so với mặt đất là bao nhiêu (làm tròn đến hàng phần trăm)?
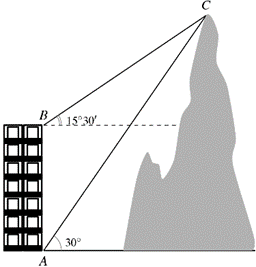
Từ hai vị trí A và B của một tòa nhà, người ta quan sát đỉnh C của ngọn núi. Biết rằng độ cao AB = 70 m, phương nhìn AC tạo với phương nằm ngang góc 30°, phương nhìn BC tạo với phương nằm ngang góc 15°30'. Ngọn núi đó có độ cao so với mặt đất là bao nhiêu (làm tròn đến hàng phần trăm)?



