Câu hỏi:
01/02/2024 61Cho tam giác ABD có AB < AD < BD và \(\widehat {ADB} = 32^\circ \). Trên cạnh BD lấy điểm C sao cho AB = CA = CB. Số đo của \(\widehat {{\rm{CAD}}}\) là
A. 20°;
B. 24°;
C. 28°;
D. 32°.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: C
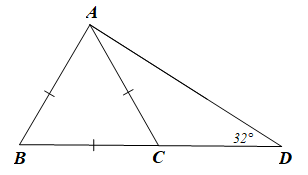
Theo hình vẽ ta có: AB = AC = BC
Suy ra ∆ABC là tam giác đều.
Suy ra \(\widehat {{\rm{ACB}}} = 60^\circ \) (tính chất tam giác đều)
Ta có \(\widehat {{\rm{ACB}}} + \widehat {{\rm{ACD}}} = 180^\circ \) (hai góc kề nhau)
Hay \(60^\circ + \widehat {{\rm{ACD}}} = 180^\circ \)
Suy ra \(\widehat {{\rm{ACD}}} = 180^\circ - 60^\circ = 120^\circ \)
Xét ∆ACD có: \(\widehat {{\rm{CAD}}} + \widehat {{\rm{ACD}}} + \widehat {\rm{D}} = 180^\circ \) (tổng ba góc trong tam giác bằng 180°)
Hay \(\widehat {{\rm{CAD}}} + 120^\circ + 32^\circ = 180^\circ \)
Suy ra \(\widehat {{\rm{CAD}}} = 180^\circ - 120^\circ - 32^\circ = 28^\circ \)
Vậy ta chọn phương án C.
Hướng dẫn giải
Đáp án đúng là: C

Theo hình vẽ ta có: AB = AC = BC
Suy ra ∆ABC là tam giác đều.
Suy ra \(\widehat {{\rm{ACB}}} = 60^\circ \) (tính chất tam giác đều)
Ta có \(\widehat {{\rm{ACB}}} + \widehat {{\rm{ACD}}} = 180^\circ \) (hai góc kề nhau)
Hay \(60^\circ + \widehat {{\rm{ACD}}} = 180^\circ \)
Suy ra \(\widehat {{\rm{ACD}}} = 180^\circ - 60^\circ = 120^\circ \)
Xét ∆ACD có: \(\widehat {{\rm{CAD}}} + \widehat {{\rm{ACD}}} + \widehat {\rm{D}} = 180^\circ \) (tổng ba góc trong tam giác bằng 180°)
Hay \(\widehat {{\rm{CAD}}} + 120^\circ + 32^\circ = 180^\circ \)
Suy ra \(\widehat {{\rm{CAD}}} = 180^\circ - 120^\circ - 32^\circ = 28^\circ \)
Vậy ta chọn phương án C.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 3:
Cho ∆ABC cân tại A có AH là tia phân giác của \(\widehat {{\rm{BAC}}}\) và \(\widehat {\rm{C}} = 52^\circ \). Số đo của \(\widehat {{\rm{BAH}}}\) là
Câu 4:
Cho ∆ABC cân tại A có \(\widehat B = 30^\circ .\) Số đo của \(\widehat C\) là
Câu 5:
Cho ∆ABC cân tại A có BC = 8 cm; chu vi của ∆ABC bằng 28 cm. Độ dài cạnh AC là
Câu 6:
Cho ∆DEF cân tại D có \(\widehat {\rm{D}} = 104^\circ \). Số đo của \(\widehat {\rm{E}}\) là