Trắc nghiệm Toán 7 CTST Bài 3. Tam giác cân có đáp án (Phần 2) (Thông hiểu)
-
210 lượt thi
-
7 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Cho ∆ABC cân tại A có \(\widehat B = 30^\circ .\) Số đo của \(\widehat C\) là
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
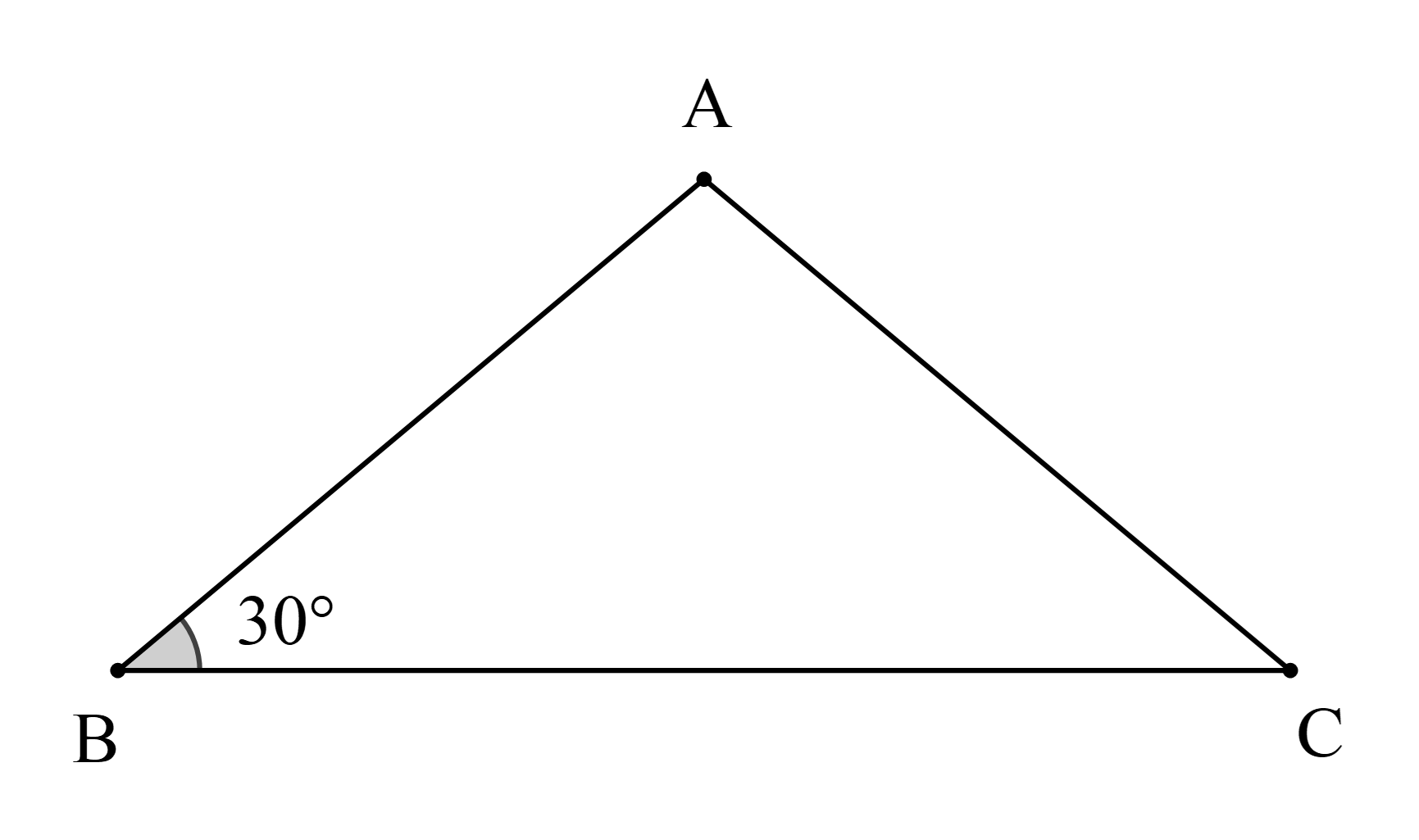
Vì ∆ABC cân tại A nên \(\widehat {\rm{C}} = \widehat {\rm{B}} = 30^\circ \) (tính chất tam giác cân).
Vậy ta chọn phương án B.
Câu 2:
Cho ∆DEF cân tại D có \(\widehat {\rm{D}} = 104^\circ \). Số đo của \(\widehat {\rm{E}}\) là
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Xét ∆DEF có: \(\widehat {\rm{D}} + \widehat {\rm{E}} + \widehat {\rm{F}} = 180^\circ \) (tổng ba góc trong một tam giác bằng 180°)
Hay \(104^\circ + \widehat {\rm{E}} + \widehat {\rm{F}} = 180^\circ \).
Suy ra \(\widehat {\rm{E}} + \widehat {\rm{F}} = 180^\circ - 104^\circ = 76^\circ \) (1)
Vì ∆DEF cân tại D nên \(\widehat {\rm{E}} = \widehat {\rm{F}}\) (tính chất tam giác cân) (2)
Từ (1) và (2) suy ra \(\widehat {\rm{E}} = \widehat {\rm{F}} = \frac{{76^\circ }}{2} = 38^\circ \).
Vậy ta chọn phương án C.
Câu 3:
Cho ∆ABC cân tại A có BC = 8 cm; chu vi của ∆ABC bằng 28 cm. Độ dài cạnh AC là
Xem đáp án
Hướng dẫn giải
Do chu vi của ∆ABC bằng 28 cm nên AB + AC + BC = 28 (cm).
Hay AB + AC + 8 = 28
Suy ra AB + AC = 28 – 8 = 20 cm (1)
Vì ∆ABC cân tại A nên AB = AC (tính chất tam giác cân) (2)
Từ (1) và (2) suy ra AB = AC = \(\frac{{20}}{2} = 10\) (cm).
Vậy ta chọn phương án A.
Câu 4:
Cho ∆ABC cân tại A có AH là tia phân giác của \(\widehat {{\rm{BAC}}}\) và \(\widehat {\rm{C}} = 52^\circ \). Số đo của \(\widehat {{\rm{BAH}}}\) là
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
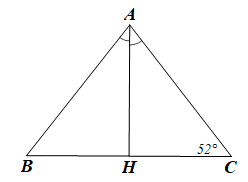
Theo bài ra ta có ∆ABC cân tại A nên \(\widehat {\rm{B}} = \widehat {\rm{C}} = 52^\circ \) (tính chất tam giác cân)
Xét ∆ABC có \(\widehat {{\rm{BAC}}} + \widehat {\rm{B}} + \widehat {\rm{C}} = 180^\circ \) (tổng ba góc trong một tam giác bằng 180°)
Hay \(\widehat {{\rm{BAC}}} + 52^\circ + 52^\circ = 180^\circ \)
Suy ra \(\widehat {{\rm{BAC}}} = 180^\circ - 52^\circ - 52^\circ = 76^\circ \)
Mà AH là tia phân giác của \(\widehat {{\rm{BAC}}}\)
Suy ra \(\widehat {{\rm{BAH}}} = \widehat {{\rm{CAH}}} = \frac{{\widehat {{\rm{BAC}}}}}{2} = \frac{{76^\circ }}{2} = 38^\circ \) (tính chất tia phân giác của một góc)
Vậy ta chọn phương án B.
Câu 5:
Cho hình vẽ
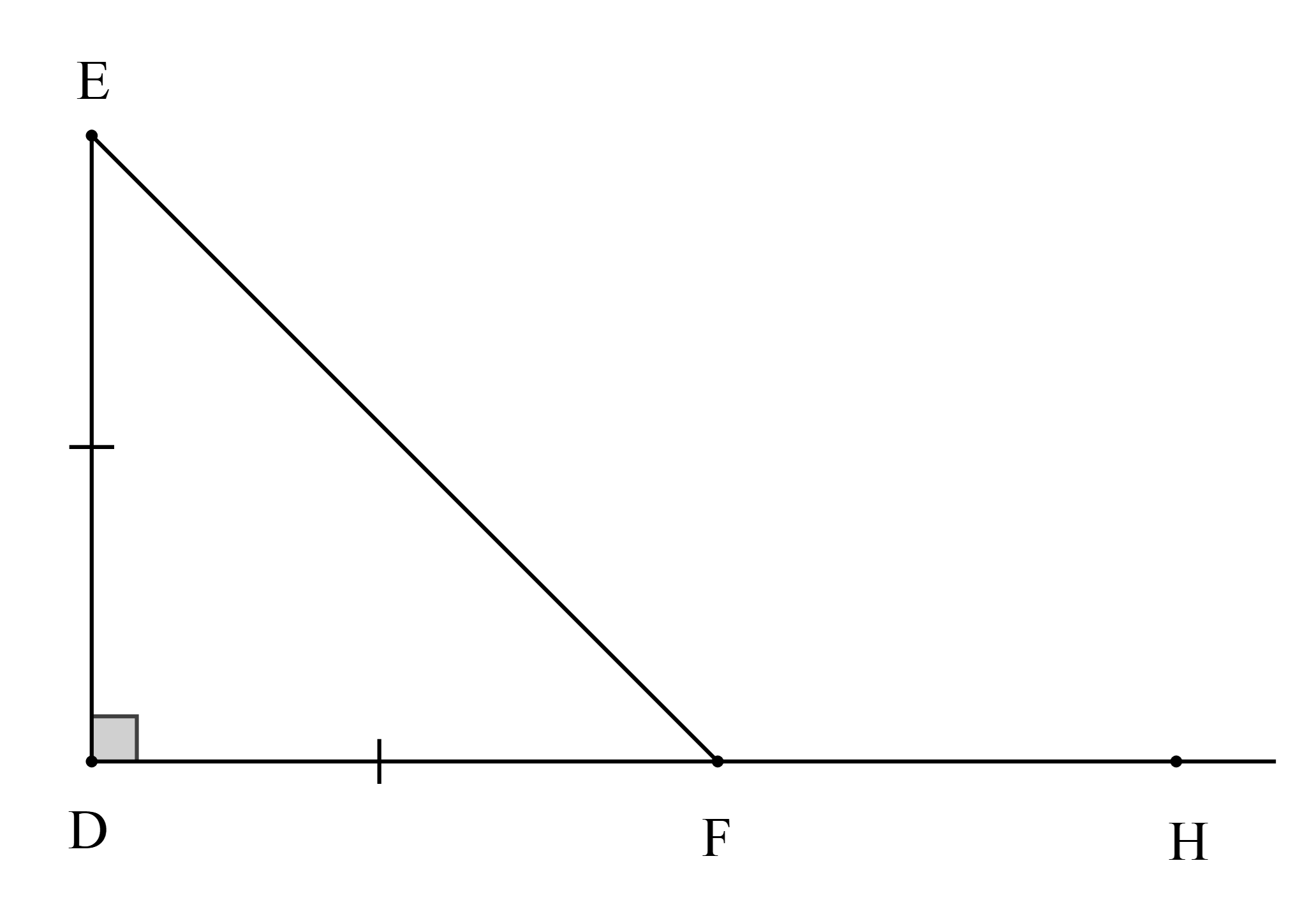
Số đo của \(\widehat {EFH}\) là
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Xét ∆DEF có DE = DF nên ∆DEF cân tại D.
Mặt khác ∆DEF cân tại D có \(\widehat {\rm{D}} = 90^\circ \)
Suy ra ∆DEF vuông cân tại D.
Suy ra \(\widehat {{\rm{DFE}}} = 45^\circ \) (tính chất tam giác vuông cân)
Ta có: \(\widehat {{\rm{DFE}}} + \widehat {EFH} = 180^\circ \) (hai góc kề nhau)
Hay \(45^\circ + \widehat {EFH} = 180^\circ \)
Suy ra \(\widehat {EFH} = 180^\circ - 45^\circ = 135^\circ \).
Vậy ta chọn phương án D.
Câu 6:
Cho tam giác ABD có AB < AD < BD và \(\widehat {ADB} = 32^\circ \). Trên cạnh BD lấy điểm C sao cho AB = CA = CB. Số đo của \(\widehat {{\rm{CAD}}}\) là
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
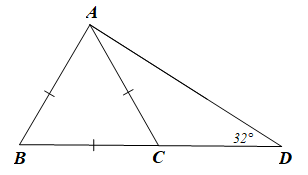
Theo hình vẽ ta có: AB = AC = BC
Suy ra ∆ABC là tam giác đều.
Suy ra \(\widehat {{\rm{ACB}}} = 60^\circ \) (tính chất tam giác đều)
Ta có \(\widehat {{\rm{ACB}}} + \widehat {{\rm{ACD}}} = 180^\circ \) (hai góc kề nhau)
Hay \(60^\circ + \widehat {{\rm{ACD}}} = 180^\circ \)
Suy ra \(\widehat {{\rm{ACD}}} = 180^\circ - 60^\circ = 120^\circ \)
Xét ∆ACD có: \(\widehat {{\rm{CAD}}} + \widehat {{\rm{ACD}}} + \widehat {\rm{D}} = 180^\circ \) (tổng ba góc trong tam giác bằng 180°)
Hay \(\widehat {{\rm{CAD}}} + 120^\circ + 32^\circ = 180^\circ \)
Suy ra \(\widehat {{\rm{CAD}}} = 180^\circ - 120^\circ - 32^\circ = 28^\circ \)
Vậy ta chọn phương án C.
Câu 7:
Cho hình vẽ sau:
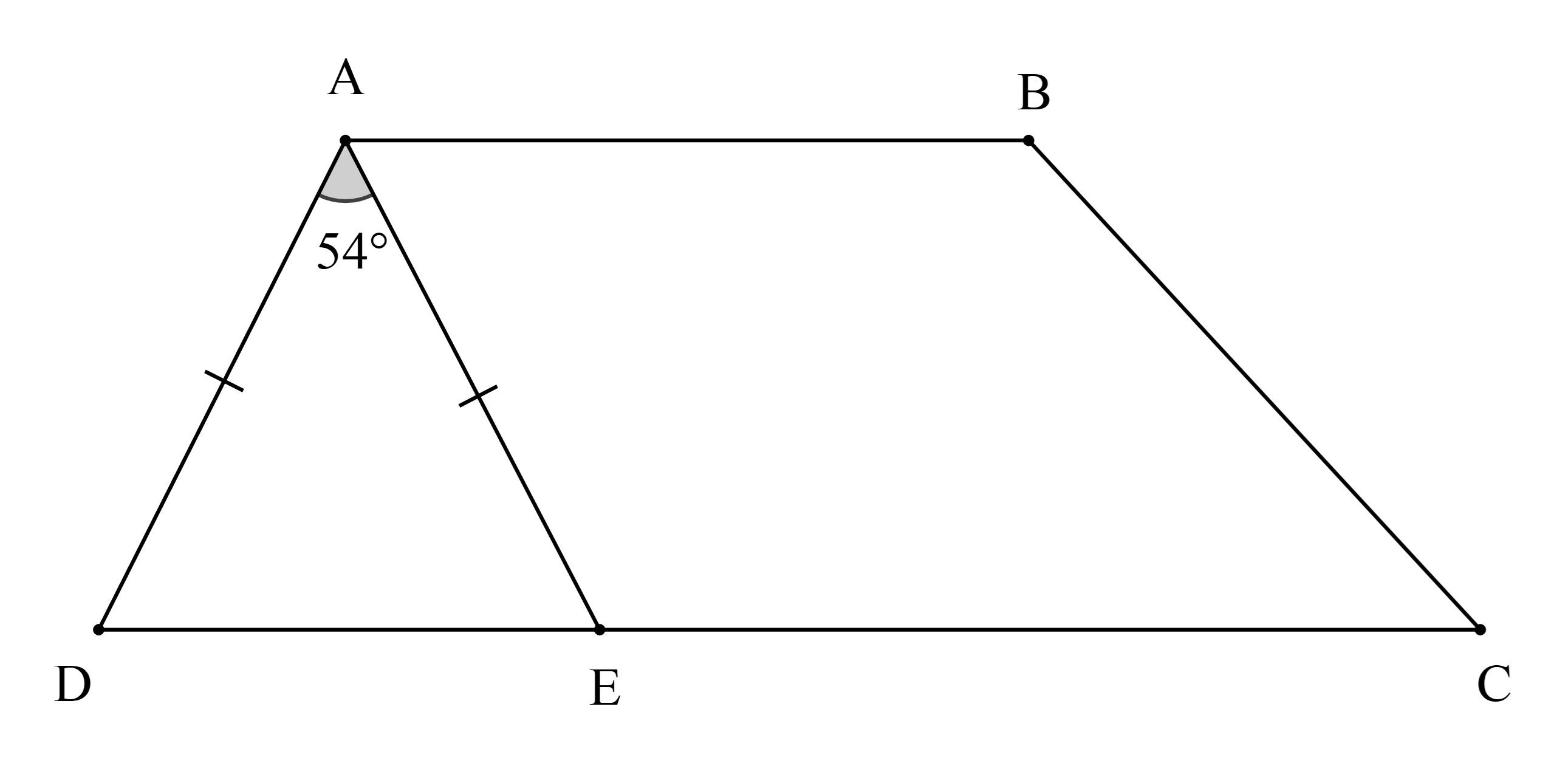
Số đo của \(\widehat {{\rm{BAE}}}\) là
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Xét ∆ADE có AD = AE (giả thiết) nên ∆ADE cân tại A.
Suy ra \(\widehat {\rm{D}} = \widehat {{\rm{AED}}}\) (1)
Xét ∆AED có: \(\widehat {\rm{D}} + \widehat {{\rm{AED}}} + \widehat {{\rm{EAD}}} = 180^\circ \)(tổng ba góc trong tam giác bằng 180°)
Hay \(\widehat {\rm{D}} + \widehat {{\rm{AED}}} + 54^\circ = 180^\circ \)
Suy ra \(\widehat {\rm{D}} + \widehat {{\rm{AED}}} = 180^\circ - 54^\circ = 126^\circ \) (2)
Từ (1) và (2) suy ra \(\widehat {\rm{D}} = \widehat {{\rm{AED}}} = \frac{{126^\circ }}{2} = 63^\circ \)
Vì AB // CD do đó \(\widehat {{\rm{BAE}}} = \widehat {{\rm{AED}}} = 63^\circ \) (hai góc so le trong).
Vậy ta chọn phương án B.