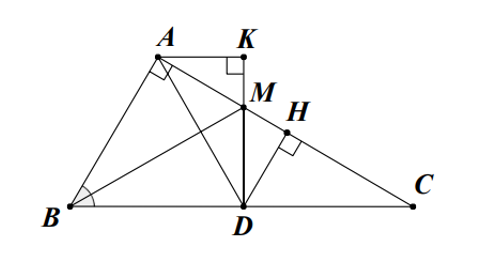
Cho tam giác ABC vuông tại A, kẻ đường phân giác BM. Trên cạnh BC lấy điểm D sao cho BD = BA. Gọi H là hình chiếu vuông góc của D trên AC, K là hình chiếu vuông góc của A trên DM. Khẳng định nào sau đây là sai?

A. BM ⊥ HK;

B. Ba đường BM, DH, AK đồng quy;

Hướng dẫn giải:

Đáp án đúng là: D

Ta có BA = BD nên ∆BAD cân tại B

Mà BM là đường phân giác nên đồng thời là đường cao, do đó BM ⊥ AD.

Do H là hình chiếu vuông góc của D trên AC, K là hình chiếu vuông góc của A trên DM.

Nên DH ⊥ AC hay DH ⊥ AM, AK ⊥ MD.

Xét ∆AMD có: MB ⊥ AD, DH ⊥ AM, AK ⊥ MD.

Suy ra BM, DH, AK là ba đường cao của ∆AMD nên chúng đồng quy.

Vậy phương án D là khẳng định sai.