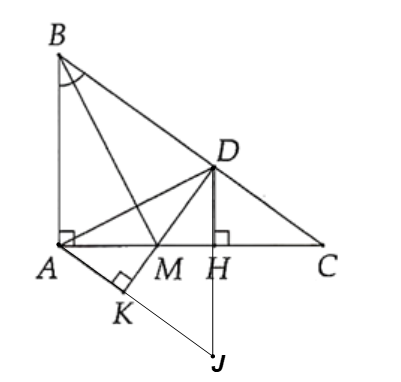
Cho tam giác ABC vuông tại A, kẻ đường phân giác BM. Trên cạnh BC lấy điểm D sao cho BD = BA. Gọi H là hình chiếu vuông góc của D trên AC, K là hình chiếu vuông góc của A trên DM. Cho các phát biểu sau:

(I) BM là đường trung trực của AD;

(II) AK, DH, BM đồng quy tại một điểm;

(III) AK // BC.

Khẳng định nào sau đây là đúng?

A. Chỉ (I) và (II) là đúng;

B. Chỉ (II) và (III) là đúng;

Hướng dẫn giải:

Đáp án đúng là: D

Vì BD = BA do đó tam giác ABD cân tại B.

Nên BM là đường phân giác cũng là đường trung trực của cạnh AD trong tam giác.

Suy ra BM ⊥ AD (1)

Kéo dài AK cắt DH tại J.

Khi đó ∆ADJ có AH ⊥ DJ, DK ⊥ AJ và AH cắt DK tại M nên M là trực tâm của ∆ADJ.

Suy ra JM ⊥ AD (2)

Từ (1) và (2) suy ra ba điểm B, M, J thẳng hàng hay AK, BM, DH là ba đường đồng quy.

Do BM là đường trung trực của AD nên MA = MD.

Xét ∆BAM và ∆BDM có:

BM là cạnh chung; BA = BD (giả thiết); MA = MD (chứng minh trên)

Do đó ∆BAM = ∆BDM (c.c.c)

Suy ra $\widehat{BAM}=\widehat{BDM}$ (hai góc tương ứng)

Mà $\widehat{BAM}=90°$ nên $\widehat{BDM}=90°$ hay MD ⊥ BC, tức DK ⊥ BC.

Lại có DK ⊥ AK tại K nên AK // BC.

Vậy cả (I), (II) và (III) đều đúng. Ta chọn phương án D.