Cho tam giác ABC cân tại A có M là trung điểm của BC. Kẻ đường thẳng d vuông góc AB
6
16/11/2024
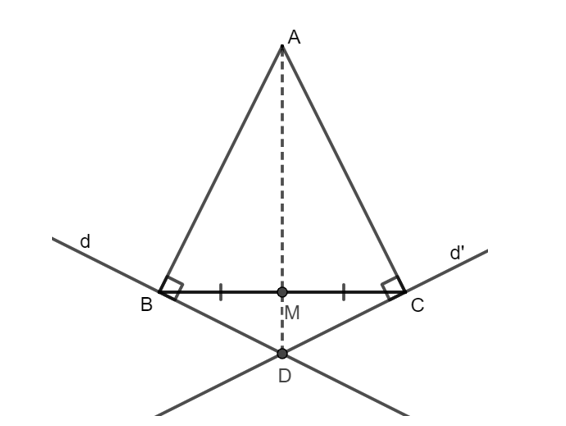
Cho tam giác ABC cân tại A có M là trung điểm của BC. Kẻ đường thẳng d vuông góc AB tại B, kẻ đường thẳng d’ vuông góc với AC tại C, hai đường thẳng d và d’ giao nhau giao tại D. Cho các khẳng định sau:
(I) A nằm trên đường trung trực của BC;
(II) Ba điểm A, M, D thẳng hàng.
Khẳng định nào sau đây là đúng nhất?
B. Chỉ có (II) đúng;
C. Cả (I) và (II) đều đúng;
D. Cả (I) và (II) đều sai.
Trả lời
Hướng dẫn giải:
Đáp án đúng là: C
Vì ∆ABC cân tại A nên AB = AC, do đó A nằm trên đường trung trực của BC (1)
Xét ∆ABD (vuông tại B) và ∆ACD (vuông tại C) có:
AB = AC (do ∆ABC cân tại A);
AD là cạnh chung
Do đó ∆ABD = ∆ACD (cạnh huyền – cạnh góc vuông)
Suy ra DB = DC (hai cạnh tương ứng)
Từ đó ta có D nằm trên đường trung trực của BC (2)
Mặt khác, M là trung điểm của BC nên M cũng nằm trên đường trung trực của BC (3)
Từ (1), (2) và (3) ta có ba điểm A, M, D nằm trên đường trung trực của BC
Suy ra ba điểm A, M, D thẳng hàng.
Vậy cả hai khẳng định (I) và (II) đều đúng. Ta chọn phương án C.