Cho tam giác ABC cân ở A, đường phân giác AK. Các đường trung trực của AB và AC cắt nhau tại O.
22
16/11/2024
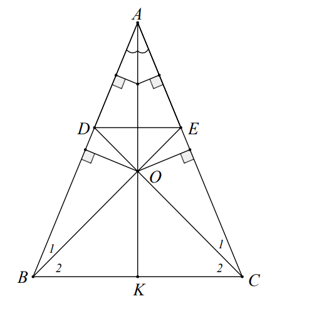
Cho tam giác ABC cân ở A, đường phân giác AK. Các đường trung trực của AB và AC cắt nhau tại O. Kéo dài CO cắt AB ở D, kéo dài BO cắt AC ở E.
Khẳng định nào sau đây là đúng?
A. Ba điểm A, K, O thẳng hàng;
B. AK là đường trung trực của BC;
C. AK và các đường trung trực của AD và AE đồng quy.
D. Cả A, B, C đều đúng.
Trả lời
Hướng dẫn giải:
Đáp án đúng là: D
Do ΔABC cân tại A nên AK là đường phân giác đồng thời là đường trung trực của BC.
Xét ΔABC có các đường trung trực của AB và AC cắt nhau tại O.
Vây thì theo tính chất ba đường trung trực của tam giác nên O thuộc đường trung trực của BC. Do đó ba điểm A, O, K thẳng hàng.
Vì O nằm trên đường trung trực của BC nên OB = OC, do đó tam giác OBC cân tại O
Suy ra ^B2=^C2
Mà ^ABC=^ACB (do ∆ABC cân ở A) nên ^B1=^C1
Xét ∆AEB và ∆ADC có:
^B1=^C1 (chứng minh trên);
^BAC là góc chung;
AB = AC (do ∆ABC cân ở A)
Từ đó ∆AEB = ∆ADC (g.c.g), suy ra AD = AE (1).
Măt khác, có OB = OC, BE = CD (vì ∆AEB = ∆ADC) nên OD = OE (2).
Từ (1) và (2) suy ra AK là đường trung trực của DE.
Xét ∆ADE, theo tính chất ba đường trung trực của tam giác suy ra AK và các đường trung
trực của AD, AE và DE đồng quy.
Vậy ta chọn phương án D.