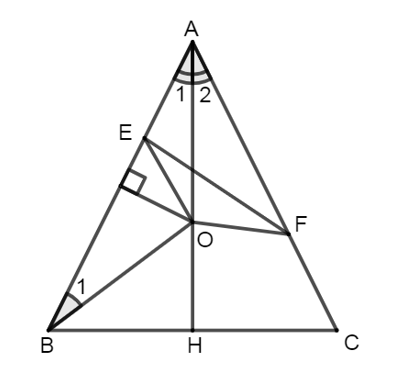
Cho tam giác ABC cân tại A có đường phân giác AH (H ∈ BC). Đường trung trực của cạnh AB cắt đường AH tại O. Trên các cạnh AB và AC lấy các điểm E và F sao cho: AE + AF = AB. Hỏi E và F ở vị trí nào để O là trung điểm của EF?

A. E, O, F thẳng hàng;

B. E, O, F cách đều ba cạnh của tam giác;

Hướng dẫn giải:

Đáp án đúng là: A

Ta có AE + AF = AB và AE + EB = AB.

Suy ra AF = EB.

Vì AH là đường phân giác nên ${\widehat{A}}_1={\widehat{A}}_2$

Vì O nằm trên đường trung trực AB nên ∆ABO cân tại O, khi đó: ${\widehat{A}}_1={\widehat{B}}_1$ và OA = OB.

Suy ra ${\widehat{A}}_2={\widehat{B}}_1.$

Xét ∆AOF và ∆BOE có:

AF = BE; ${\widehat{A}}_2={\widehat{B}}_1.$ OA = OB

Do đó ∆AOF = ∆BOE (c.g.c)

Suy ra OF = OE (hai cạnh tương ứng).

Khi đó để O là trung điểm của EF thì cần thêm điều kiện là E, O, F thẳng hàng.