Câu hỏi:
25/01/2024 115
Cho ∆ABC vuông tại A có AB < AC. Kẻ AH vuông góc với BC (H ∈ BC). Gọi D là điểm trên cạnh AC sao cho AD = AB. Vẽ DE vuông góc với BC (E ∈ BC) và DK vuông góc với AH (K ∈ AH). Độ dài của HE bằng:
Cho ∆ABC vuông tại A có AB < AC. Kẻ AH vuông góc với BC (H ∈ BC). Gọi D là điểm trên cạnh AC sao cho AD = AB. Vẽ DE vuông góc với BC (E ∈ BC) và DK vuông góc với AH (K ∈ AH). Độ dài của HE bằng:
A. HA;
A. HA;
B. KD;
B. KD;
C. Cả A và B đều đúng;
D. Cả A và B đều sai.
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: C
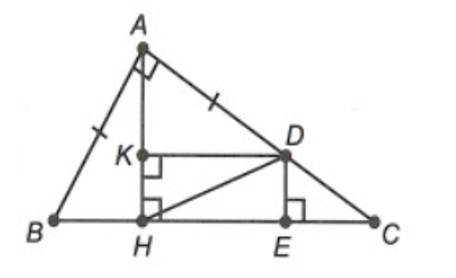
Xét ∆HAB và ∆KDA, có:
AB = AD (giả thiết)
.
(cùng phụ với ).
Do đó ∆HAB = ∆KDA (cạnh huyền – góc nhọn)
Suy ra HA = KD (cặp cạnh tương ứng)
Vì vậy phương án B, D đúng.
Ta có KD ⊥ AH (giả thiết) và EH ⊥ AH (giả thiết)
Suy ra KD // EH.
Suy ra (cặp góc so le trong).
Xét ∆KDH và ∆EHD, có:
.
DH là cạnh chung.
(chứng minh trên)
Do đó ∆KDH = ∆EHD (cạnh huyền – góc nhọn)
Suy ra KD = HE (cặp cạnh tương ứng)
Mà HA = KD (chứng minh trên)
Do đó HA = HE.
Vì vậy phương án C đúng.
Hướng dẫn giải
Đáp án đúng là: C
Xét ∆HAB và ∆KDA, có:
AB = AD (giả thiết)
.
(cùng phụ với ).
Do đó ∆HAB = ∆KDA (cạnh huyền – góc nhọn)
Suy ra HA = KD (cặp cạnh tương ứng)
Vì vậy phương án B, D đúng.
Ta có KD ⊥ AH (giả thiết) và EH ⊥ AH (giả thiết)
Suy ra KD // EH.
Suy ra (cặp góc so le trong).
Xét ∆KDH và ∆EHD, có:
.
DH là cạnh chung.
(chứng minh trên)
Do đó ∆KDH = ∆EHD (cạnh huyền – góc nhọn)
Suy ra KD = HE (cặp cạnh tương ứng)
Mà HA = KD (chứng minh trên)
Do đó HA = HE.
Vì vậy phương án C đúng.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho ∆ABC có AB = AC (). Vẽ BH ⊥ AC (H ∈ AC), CK ⊥ AB (K ∈ AB). Gọi I là giao điểm của BH và CK. Gọi D là giao điểm của AI và BC. Ta có các phát biểu sau:
(I) AI là tia phân giác của ;
(II) AD ⊥ BC;
(III) D là trung điểm của BC.
Phát biểu đúng là:
Cho ∆ABC có AB = AC (). Vẽ BH ⊥ AC (H ∈ AC), CK ⊥ AB (K ∈ AB). Gọi I là giao điểm của BH và CK. Gọi D là giao điểm của AI và BC. Ta có các phát biểu sau:
(I) AI là tia phân giác của ;
(II) AD ⊥ BC;
(III) D là trung điểm của BC.
Phát biểu đúng là:
Câu 2:
Cho đoạn thẳng AB, điểm O nằm giữa A và B. Kẻ tia Ox vuông góc với AB. Trên tia Ox lấy các điểm C và D sao cho OC = OA, OD = OB. Gọi M, N lần lượt là trung điểm của AD và BC. Góc MON là:
Cho đoạn thẳng AB, điểm O nằm giữa A và B. Kẻ tia Ox vuông góc với AB. Trên tia Ox lấy các điểm C và D sao cho OC = OA, OD = OB. Gọi M, N lần lượt là trung điểm của AD và BC. Góc MON là:
