Cho tam giác ABC với AB = 6 cm, AC = 9 cm.

a) Lấy điểm M, N lần lượt trên các cạnh AB, AC sao cho AM = 4 cm, AN = 6 cm. Chứng minh rằng ∆AMN ᔕ ∆ABC và tìm tỉ số đồng dạng.

b) Lấy điểm P trên cạnh AC sao cho AP = 4 cm. Chứng minh rằng ∆APB ᔕ ∆ABC.

Lời giải

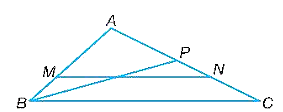
a)

Xét tam giác ABC có:

\(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\,\,\,\,\,\,\left( {do\,\,\frac{4}{6} = \frac{6}{9} = \frac{2}{3}} \right)\)

Suy ra MN song song với BC (định lí Thalès đảo)

Do ∆AMN ᔕ ∆ABC với tỉ số đồng dạng \(\frac{2}{3}\) (1).

b)

Tam giác APB và tam giác AMN có:

AP = AM (= 4 cm)

\(\widehat A\) chung

AB = AN (= 6 cm)

Do đó, ∆APB = ∆AMN (c.g.c). Suy ra ∆APB ᔕ ∆AMN (2).

Từ (1) và (2) ta có: ∆APB ᔕ ∆ABC.