Cho hình bình hành ABCD và cho E, F lần lượt là trung điểm của AB và AC. Chứng minh rằng ∆AEF ᔕ ∆CDA.
Cho hình bình hành ABCD và cho E, F lần lượt là trung điểm của AB và AC. Chứng minh rằng ∆AEF ᔕ ∆CDA.
Lời giải
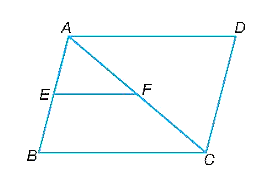
Vì ABCD là hình bình hành nên ˆB=ˆD, AB = CD, BC = AD.
Do đó, ∆ABC = ∆CDA (c.g.c). Suy ra ∆ABC ᔕ ∆CDA (1).
Tam giác ABC có E, F lần lượt là trung điểm của AB và AC nên EF là đường trung bình tam giác ABC. Do đó, EF // BC.
Tam giác ABC có:
EF // BC nên ∆AEF ᔕ ∆ABC (2).
Từ (1) và (2) suy ra: ∆AEF ᔕ ∆CDA.