Cho tam giác ABC nhọn có các đường cao BD chứng minh Tứ giác MNHK là hình thoi
26
18/08/2024
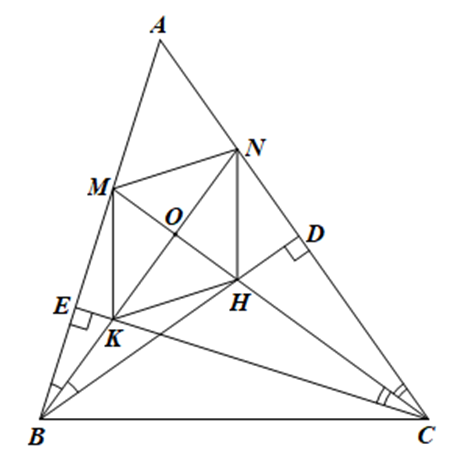
Cho tam giác ABC nhọn có các đường cao BD, CE. Tia phân giác của các góc ACE, ABD cắt nhau tại O và cắt AB, AC lần lượt tại M, N. Tia BN cắt CE tại K, tia CM cắt BD tại H. Chứng minh:
Tứ giác MNHK là hình thoi.
Trả lời
Xét ∆BMO vuông tại O và ∆BHO vuông tại O có:
Cạnh BO chung, ^MBO=^HBO
Do đó ∆BMO = ∆BHO (cạnh góc vuông – góc nhọn kề).
Suy ra OM = OH (hai cạnh tương ứng)
Hay O là trung điểm của MH.
Tương tự ta chứng minh được ∆CNO = ∆CKO (cạnh góc vuông – góc nhọn kề).
Suy ra ON = OK (hai cạnh tương ứng)
Hay O là trung điểm của NK.
Tứ giác MNHK có hai đường chéo MH và NK cắt nhau tại trung điểm O của mỗi đường nên MNHK là hình bình hành.
Hình bình hành MNHK có MH ⊥ NK nên MNHK là hình thoi.