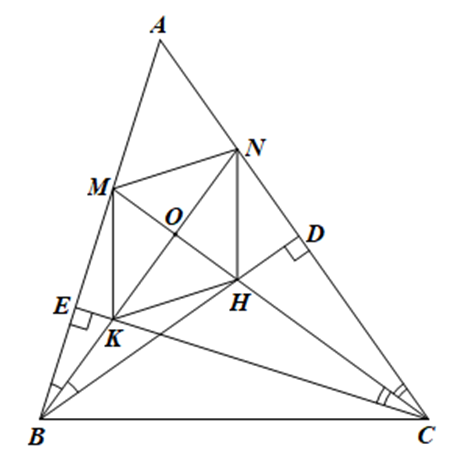
Cho tam giác ABC nhọn có các đường cao BD, CE Chứng minh BN vuông góc CM
Cho tam giác ABC nhọn có các đường cao BD, CE. Tia phân giác của các góc ACE, ABD cắt nhau tại O và cắt AB, AC lần lượt tại M, N. Tia BN cắt CE tại K, tia CM cắt BD tại H. Chứng minh:
BN ⊥ CM;