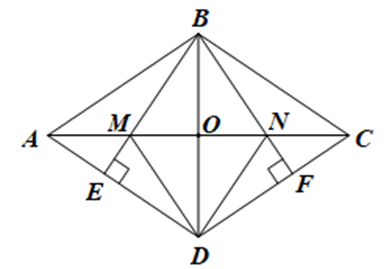
Gọi O là giao điểm của AC và BD.
Do ABCD là hình thoi nên AC vuông góc với BD tại trung điểm O của BD.
Suy ra AC là đường trung trực của BD. Do đó BM = DM, BN = DN.
Do ABCD là hình thoi nên BA = BC, ^BAE=^BCF.
Xét ∆ABE vuông tại E và ∆BCF vuông tại F có:
BA = BC, ^BAE=^BCF.
Do đó ∆ABE = ∆BCF (cạnh huyền – góc nhọn).
Suy ra ^ABE=^CBF (hai góc tương ứng)
Mà ^ABD=^CBD (do ABCD là hình thoi nên BD là đường phân giác của góc ABC) , suy ra ^MBO=^NBO.
Xét ∆MBO vuông tại O và ∆NBO vuông tại O có:
^MBO=^NBO, cạnh BO chung
Do đó ∆MBO = ∆NBO (cạnh góc vuông – góc nhọn kề).
Suy ra BM = BN (hai cạnh tương ứng)
Mà BM = DM và BN = DN, suy ra BM = DM = BN = DN.
Tứ giác BMDN có BM = DM = BN = DN nên BMDN là hình thoi.