Cho hình thoi ABCD có AB = 2 cm Chứng minh DH + DK không đổi
Cho hình thoi ABCD có AB = 2 cm, ˆA=12ˆB. Các điểm H, K thay đổi lần lượt trên cạnh AD, CD sao cho ^HBK=60∘.
Chứng minh DH + DK không đổi.
Cho hình thoi ABCD có AB = 2 cm, ˆA=12ˆB. Các điểm H, K thay đổi lần lượt trên cạnh AD, CD sao cho ^HBK=60∘.
Chứng minh DH + DK không đổi.
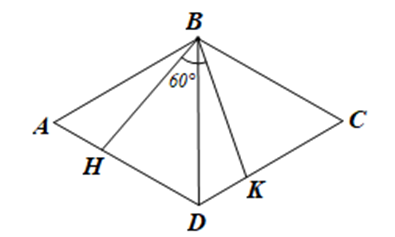
Do ABCD là hình thoi nên DA = AB = 2 cm, ^ABD=^CBD=12^ABC (BD là đường phân giác của góc ABC).
Mà ^BAD=12^ABC, suy ra ^BAD=^ABD.
Do đó tam giác ABD cân tại D.
Suy ra DA = DB.
Mà AB = DA, suy ra AB = DA = DB.
Do đó tam giác ABD đều nên ^BAD=^ABD=^ADB=60∘.
Suy ra ^BDC=^ABD=60∘ (hai góc so le trong của AB // CD).
Ta có: ^ABH+^HBD=^ABD=60∘; ^HBD+^DBK=^HBK=60∘
Suy ra ^ABH=^DBK.
Xét ∆ABH và ∆DBK có:
^ABH=^DBK; AB = BD; ^BAH=^BDK(=60∘)
Do đó ∆ABH = ∆DBK (g.c.g).
Suy ra AH = DK (hai cạnh tương ứng).
Do đó DH + DK = DH + AH = AD (không đổi)
Vậy DH + DK không đổi.