Cho tam giác ABC không vuông tại A. Dựng bên ngoài tam giác đó hai tam giác ABD, ACE vuông cân tại đỉnh A rồi dựng hình bình hành AEID.

a) Chứng minh hai tam giác ABC và DAI bằng nhau.

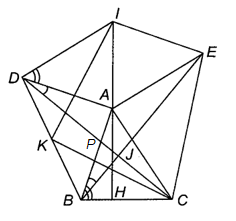
a) Hình bình hành AEID có  $\widehat{ADI}+\widehat{DAE}=180°$ (hai góc kề một cạnh của hình bình hành)

Ta có:  $\widehat{DAE}+\widehat{DAB}+\widehat{BAC}+\widehat{CAE}=360°$

Mà ∆ABD vuông tại A, ∆ACE vuông tại A, suy ra  $\widehat{DAB}=\widehat{CAE}=90°$

Suy ra  $\widehat{BAC}+\widehat{DAE}=360°-90°-90°=180°$ 

Vậy  $\widehat{ADI}=\widehat{BAC.}$

Do ∆ABD vuông cân tại A nên AD = AB

∆ACE vuông cân tại A nên AC = AE

Mà AEID là hình bình hành nên AE = DI, do đó DI = AC.

Xét ∆ADI và ∆BAC có

AD = AB,  $\widehat{ADI}=\widehat{BAC}$, DI = AC (chứng minh trên)

Suy ra ∆ADI = ∆BAC (c.g.c).