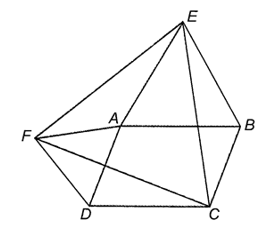
Do ABCD là hình bình hành nên AB // CD
Gọi
Vì AB // CD nên ta có
Suy ra
(do ∆AFD nên ) (1)
• Ta có:
Suy ra
Mà (do ∆AFD và ∆ABE đều)
Suy ra
Từ (1) và (2) suy ra
Xét ∆AEF và ∆DCF có
AF = DF ( vì ∆ADF đều);
(chứng minh trên);
AE = DC (vì cùng bằng AB)
Do đó: ∆AEF = ∆DCF (c.g.c)
Suy ra EF = CF (*)
•
Mà ABCD là hình bình hành nên
Suy ra , mà (chứng minh trên)
Suy ra
Xét ΔBCE và ΔDFC có:
BE = CD (vì cùng bằng AB);
(chứng minh trên);
BC = DF (vì cùng bằng AD)
Do đó ∆BCE = ∆DFC (c.g.c)
Suy ra CE = CF (**)
Từ (*) và (**) suy ra: EF = CF = CE
Vậy ∆ECF là tam giác đều.