Cho hình bình hành ABCD. Lấy các điểm E thuộc AB, F thuộc CD sao cho AE = CF; lấy các điểm G thuộc BC, H thuộc AD sao cho BG = DH. Chứng minh EGFH là một hình bình hành và các đường thẳng AC, BD, EF, GH đồng quy.

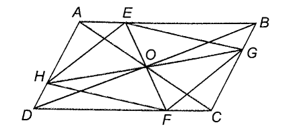
Do ABCD là hình bình hành nên  $\widehat{BAD}=\widehat{BCD}$, AD = BC, AB = CD,  $\widehat{ABC}=\widehat{ADC}$

• Ta có: AD = AH + DH, BC = BG +  CG

Mà BG = DH, AD = BC nên AH = CG

Xét ∆AEH và ∆CFG có:

AH = CG,  $\widehat{EAH}=\widehat{FCG}$ (do  $\widehat{BAD}=\widehat{BCD}$), AE = CF

Suy ra ∆AEH = ∆CFG (c.g.c) nên EH = FG.

Ta có: AB = AE + BE, CD = CF + DF

Mà AB = CD, AE = CF nên BE = DF

Xét ∆BEG và ∆DFH có:

BE = DF,  $\widehat{EBG}=\widehat{HDF}$ (do  $\widehat{ABC}=\widehat{ADC}$), BG = DH

Suy ra ∆BEG = ∆DFH (c.g.c) nên EG = FH.

Tứ giác EGFH có EH = FG, EG = FH nên là một hình bình hành.

• Do ABCD là hình bình hành nên khi ta gọi O là giao điểm của AC thì O là trung điểm của BD.

Vì tứ giác BEDF là hình bình hành (do EB = DF và EB // DF) nên hai đường chéo EF cắt nhau DB tại trung điểm O của BD.

Tương tự, GH đi qua trung điểm O của BD.

Vậy các đường thẳng AC, BD, EF, GH đồng quy.