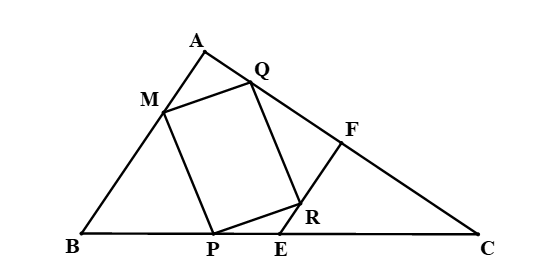
Cho tam giác ABC có E, F lần lượt là trung điểm của BC, AC. Các điểm M, P, R, Q lần lượt nằm trên AB, BE, EF, FA sao cho $\frac{BM}{MA}=\frac{QF}{QA}=\frac{RF}{RE}=\frac{BP}{PE}=\frac{9}{5}$.

A. 0;

B. 1;

Hướng dẫn giải:

Đáp án đúng là: C

*) Ta có:

+ Hai đường thẳng AF và BE cùng đi qua điểm C.

+ $\frac{\text{AF}}{AC}=\frac{\text{BE}}{BC}=\frac{1}{2}$ (vì F, F lần lượt là trung điểm của BC, AC).

Þ Hai đoạn thẳng FE và AB đồng dạng phối cảnh, điểm C là tâm đồng dạng phối cảnh.

Þ Khẳng định (I) đúng.

*) $\frac{BM}{MA}=\frac{QF}{QA}=\frac{RF}{RE}=\frac{BP}{PE}=\frac{9}{5}$

Vì $\frac{BM}{MA}=\frac{9}{5}\Rightarrow \frac{BM}{BA}=\frac{9}{14}$ do đó khẳng định II sai.

*) Ta có:

+ Hai đường thẳng BP và FR cùng đi qua điểm E.

+) $\frac{RF}{RE}=\frac{BP}{PE}=\frac{9}{5}\Rightarrow \frac{BE}{PE}=\frac{FE}{\text{RE}}=\frac{14}{5}$

Þ Hai đoạn thẳng PR và BF đồng dạng phối cảnh, điểm E là tâm đồng dạng phối cảnh.

Vậy khẳng định (I) và (II) đúng.