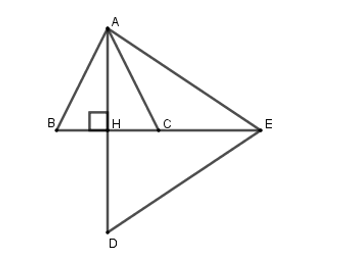
Cho tam giác ABC cân tại A. Vẽ AH ⊥ BC. Trên tia đối của tia HA lấy điểm D sao cho HD = HA. Trên tia đối của tia CB lấy điểm E sao cho CE = CB. Điểm C là trọng tâm của tam giác nào?

A. ΔABD;

B. ΔADE;

Hướng dẫn giải:

Đáp án đúng là: B

Xét ∆AHB (vuông tại H) và AHC (vuông tại H) có:

AB = AC (do ΔABC cân tại A);

AH là cạnh chung

Do đó: ΔAHB = ΔAHC (cạnh huyền – cạnh góc vuông)

Suy ra HB = HC (hai cạnh tương ứng)

Ta có CE = CB = HB + HC = 2CH

Xét ΔADE có EH là đường trung tuyến mà CE = 2CH nên C là trọng tâm của ΔADE.