Cho ΔABC có hai đường trung tuyến BN, CP vuông góc với nhau tại G. Biết độ dài

C. 5cm;

Trả lời

Hướng dẫn giải:

Đáp án đúng là: C

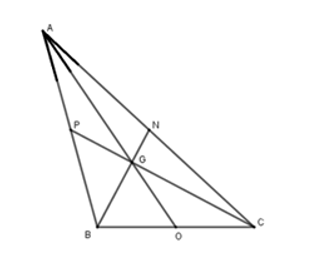
Xét ∆ABC có hai đường trung tuyến BN, CP cắt nhau tại G nên G là trọng tâm của ∆ABC. Do đó AG là đường trung tuyến thứ ba của tam giác.

Giả sử AG cắt BC tại O.

Khi đó O là trung điểm của BC nên GO là đường trung tuyến của ∆GBC.

Xét ΔBGC vuông tại G (do $\widehat{BGC}=90°),$ có GO là đường trung tuyến của ∆GBC nên theo kết quả của Ví dụ 2, ta suy ra $OG=OB=OC=\frac{1}{2}BC.$

Mà $OG=\frac{1}{2}AG$ (do G là trọng tâm của ∆ABC)

Suy ra AG = BC = 5 (cm).