A. cân tại G;

B. vuông tại G;

Hướng dẫn giải:

Đáp án đúng là: A

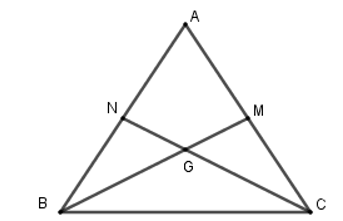
Vì ΔABC cân tại A nên AB = AC.

Ta có M là trung điểm của AC suy ra $AM=MC=\frac{1}{2}AC$.

Ta có N là trung điểm của AC suy ra $AN=NB=\frac{1}{2}AB$.

Do đó: AM = MC = AN = NB.

Xét ΔABM và ΔACN có:

AB = AC (chứng minh trên);

$\widehat{A}$ là góc chung;

AM = AN (chứng minh trên)

Do đó ΔABM và ΔACN (c.g.c)

Suy ra BM = CN (hai cạnh tương ứng)

Vì G là trọng tâm của ΔABC nên $BG=\frac{2}{3}BM;CG=\frac{2}{3}CN$

Do đó BG = CG hay tam giác BGC cân tại G.