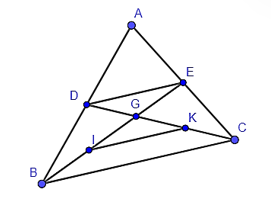
Cho tam giác ABC, các đường trung tuyến BE và CD cắt nhau tại G. Gọi I, K theo thứ tự là trung điểm của GB, GC. Đoạn thẳng DE song song và bằng với đoạn thẳng nào?

Đáp án đúng là: B

Trong tam giác ABC có D là trung điểm AB, E là trung điểm AC.

Do đó DE là đường trung bình của tam giác ABC.

Suy ra DE // BC và $\text{DE}=\frac{1}{2}\text{BC}$  (tính chất đường trung bình của tam giác) (1).

Trong tam giác GBC có I là trung điểm GB, K là trung điểm GC.

Do đó IK là đường trung bình của tam giác GBC.

Suy ra IK // BC và $\text{IK}=\frac{1}{2}\text{BC}$  (tính chất đường trung bình của tam giác) (2).

Từ (1) và (2) suy ra IK // DE và IK = DE.