Cho hình vuông ABCD, điểm E thuộc cạnh CD. Tia phân giác của $\widehat{ABE}$  cắt AD ở K. Chứng minh rằng: AK + CE = BE.

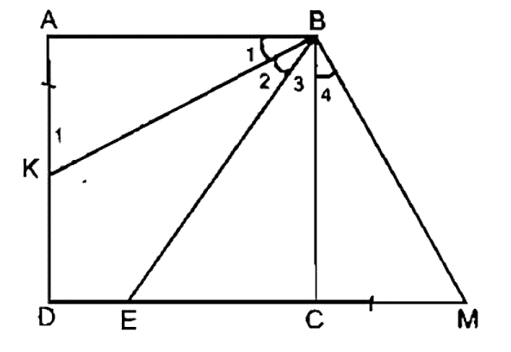
Trên tia đối CD lấy điểm M sao cho CM = AK

Ta có: AK + CE = CM + CE = EM (*)

Xét tam giác ABK và tam giác CBM có:

AB = CB (gt)

$\widehat{A}=\widehat{C}=90°$

AK = CM (theo cách vẽ)

Do đó, tam giác ABK bằng tam giác CBM (c.g.c)

$\Rightarrow \widehat{B_1}=\widehat{B{\text{}}_4}$ (1)

$\widehat{KBC}=90°-\widehat{B_1}$ (2)

Trong tam giác CBM vuông tại C

$\widehat{M}=90°-\widehat{B_4}$

Từ (1), (2), (3) ta có: $\widehat{KBC}=\widehat{M}$  (4)

$\widehat{KBC}=\widehat{B_2}+\widehat{B_3}$ mà $\widehat{B_1}=\widehat{B_2}$  (gt)

$\widehat{B_1}=\widehat{B_4}$ (chứng minh trên)

$\Rightarrow \widehat{B_2}=\widehat{B_4}\Rightarrow \widehat{B_2}+\widehat{B_3}=\widehat{B_4}+\widehat{B_3}\Rightarrow \widehat{KBC}=\widehat{EBM}$ (5)

Từ (4) và (5) suy ra: $\widehat{EBM}=\widehat{M}$

Do đó, tam giác EBM cân tại E

 (**)

Từ (*) và (**) suy ra: AK + CE = BE.