Cho hình thang ABCD (AB // CD) có E và F lần lượt là trung điểm hai cạnh bên AD và BC

Bài 4 trang 54 Toán 8 Tập 2: Cho hình thang ABCD (AB // CD) có E và F lần lượt là trung điểm hai cạnh bên AD và BC. Gọi K là giao điểm của AF và DC (Hình 12).

a) Tam giác FBA và tam giác FCK có bằng nhau không? Vì sao?

b) Chứng minh EF // CD // AB.

c) Chứng minh $\mathrm{EF}=\frac{A\mathrm{B}+CD}{2}$

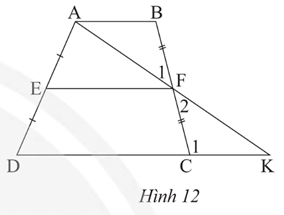
Trả lời

a) Xét tam giác FBA và FCK ta có:

$\widehat{F_1}=\widehat{F_2}$ (hai góc đối đỉnh)

FB = FC (giả thiết)

$\widehat{FBA}=\widehat{FCK}$ (AB // CD, hai góc so le trong)

Do đó ΔFBA = ΔFCK (g.c.g)

b) ΔFBA = ΔFCK suy ra FA = FK

Xét tam giác ADK có:

EA = ED

FA = FK

Do đó, EF là đường trng bình tam giác ABC.

Suy ra EF // DK

Mà AB // CD nên EF // CD // AB.

c) EF là đường trung bình tam giác ADK.

Suy ra $EF=\frac{1}{2}DK=\frac{1}{2}(CD+CK)$

Mà CK = BA (do ΔFBA = ΔFCK)

Do đó $\mathrm{EF}=\frac{A\mathrm{B}+CD}{2}$

Xem thêm các bài giải SGK Toán lớp 8 Chân trời sáng tạo hay, chi tiết khác:

Bài tập cuối chương 6

Bài 1: Định lí Thalès trong tam giác

Bài 2: Đường trung bình của tam giác

Bài 3: Tính chất đường phân giác của tam giác

Bài tập cuối chương 7

Bài 1: Hai tam giác đồng dạng