Cho hình lập phương MNPQ.M’N’P’Q’ có cạnh bằng a. a) Góc giữa hai đường thẳng MN và M’P’ bằng

Bài 1 trang 116 Toán 11 Tập 2: Cho hình lập phương MNPQ.M’N’P’Q’ có cạnh bằng a.

a) Góc giữa hai đường thẳng MN và M’P’ bằng:

A. 30°;

B. 45°;

C. 60°;

D. 90°.

b) Gọi α là số đo góc giữa đường thẳng M’P và mặt phẳng (MNPQ). Giá trị tanα bằng:

A. 1;

B. 2;

C. $\sqrt{2};$

D. $\frac{1}{\sqrt{2}}.$

c) Số đo của góc nhị diện [N, MM’, P] bằng:

A. 30°;

B. 45°;

C. 60°;

D. 90°.

d) Khoảng cách từ điểm M đến mặt phẳng (NQQ’N’) bằng:

A. a;

B. $\frac{a}{\sqrt{2}};$

C. $a\sqrt{2};$

D. $\frac{a}{2}.$

Trả lời

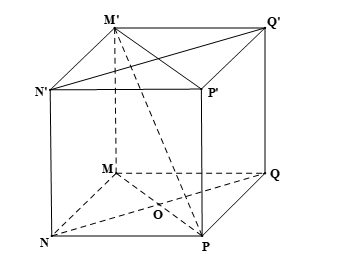
a) Đáp án đúng là: B

Vì MNPQ.M’N’P’Q’ là hình lập phương nên MM’ // PP’ và MM’ = PP’.

Suy ra M’P’PM là hình bình hành. Do đó MP // M’P’.

Suy ra góc giữa hai đường thẳng MN và M’P’ bằng góc giữa hai đường thẳng MN và MP và bằng $\widehat{NMP}.$

Vì MNPQ là hình vuông nên đường chéo MP là đường phân giác của góc NMQ, do đó $\widehat{NMP}=45°.$

Vậy góc giữa hai đường thẳng MN và M’P’ bằng 45°.

b) Đáp án đúng là: D

Vì MNPQ.M’N’P’Q’ là hình lập phương nên M’M ⊥ (MNPQ).

Khi đó, MP là hình chiếu của M’P trên (MNPQ).

Suy ra góc giữa đường thẳng M’P và mặt phẳng (MNPQ) bằng $\widehat{M^{\text{'}}PM}$, tức là $\alpha =\widehat{M^{\text{'}}PM}.$

Vì MNPQ là hình vuông nên $\widehat{MNP}=90°,$ do đó tam giác MNP vuông tại N.

Áp dụng định lí Pythagore trong tam giác MNP vuông tại N có:

MP² = MN² + NP² = a² + a² = 2a²

Suy ra $MP=a\sqrt{2}.$

Do M’M ⊥ (MNPQ) và MP ⊂ (MNPQ) nên M’M ⊥ MP.

Xét ∆M’PM vuông tại M (do M’M ⊥ MP) có:

$\tan \widehat{M^{\text{'}}PM}=\frac{M^{\text{'}}M}{MP}=\frac{a}{a\sqrt{2}}=\frac{1}{\sqrt{2}}.$

Suy ra $\tan \alpha =\frac{1}{\sqrt{2}}$ với $\alpha =\widehat{MP{M}^{\text{'}}}.$

c) Đáp án đúng là: B

Do M’M ⊥ (MNPQ) và MN ⊂ (MNPQ), MP ⊂ (MNPQ).

Suy ra M’M ⊥ MN và M’M ⊥ MP.

Mà MN ∩ MP = M ∈ M’M.

Do đó $\widehat{NMP}$ là góc phẳng nhị diện của góc nhị diện [N, MM’, P].

Theo câu a ta có $\widehat{NMP}=45°.$

Vậy số đo của góc nhị diện [N, MM’, P] bằng 45°.

d) Đáp án đúng là: B

Gọi O là giao điểm của MP và NQ.

Vì MNPQ là hình vuông nên MO ⊥ NQ.

Do MNPQ.M’N’P’Q’ là hình lập phương nên N’N ⊥ (MNPQ).

Mà MO ⊂ (MNPQ) nên N’N ⊥ MO.

Ta có: MO ⊥ NQ, MO ⊥ N’N và NQ ∩ N’N = N trong (NQQ’N’).

Suy ra MO ⊥ (NQQ’N’).

Khi đó, d(M, (NQQ’N’)) = MO.

Vì MNPQ là hình vuông và O = MP ∩ NQ nên O là trung điểm của MP.

Do đó $MO=\frac{MP}{2}=\frac{a\sqrt{2}}{2}=\frac{a}{\sqrt{2}}.$

Vậy khoảng cách từ điểm M đến mặt phẳng (NQQ’N’) bằng $\frac{a}{\sqrt{2}}.$

Xem thêm các bài giải SGK Toán lớp 11 Cánh diều hay, chi tiết khác: