Cho hình lăng trụ tam giác đều ABC.A’B’C’ có tất cả các cạnh bằng a. Gọi M là trung điểm của AB

Bài 7 trang 117 Toán 11 Tập 2: Cho hình lăng trụ tam giác đều ABC.A’B’C’ có tất cả các cạnh bằng a. Gọi M là trung điểm của AB (Hình 100).

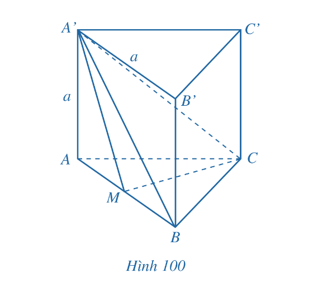
a) Tính góc giữa hai đường thẳng AB và B’C’.

b) Tính góc giữa đường thẳng A’B và mặt phẳng (ABC).

c) Tính số đo của góc nhị diện [B, CC’, M].

d) Chứng minh rằng CC’ // (ABB’A’). Tính khoảng cách giữa đường thẳng CC’ và mặt phẳng (ABB’A’).

e) Chứng minh rằng CM ⊥ (ABB’A’). Tính khoảng cách giữa hai đường thẳng CC’ và A’M.

g) Tính thể tích của khối lăng trụ tam giác đều ABC.A’B’C’ và thể tích khối chóp A’.MBC.

Trả lời

Vì ABC.A’B’C’ là hình lăng trụ tam giác đều có tất cả các cạnh bằng a nên ta có:

⦁ Các mặt bên A’C’CA, B’C’CB, A’B’BA đều là hình vuông cạnh a.

⦁ Hai mặt đáy ABC và A’B’C’ là hai tam giác đều cạnh a và hai mặt phẳng chứa hai mặt đáy song song với nhau.

⦁ Các cạnh bên AA’, BB’, CC’ đều vuông góc với mặt phẳng đáy (ABC) và (A’B’C’).

a) Do B’C’CB là hình vuông nên BC // B’C’.

Suy ra góc giữa hai đường thẳng AB và B’C’ bằng góc giữa hai đường thẳng AB và BC và bằng $\widehat{ABC}.$

Mặt khác ABC là tam giác đều nên $\widehat{ABC}=60°.$

Vậy góc giữa hai đường thẳng AB và B’C’ bằng 60°.

b) Vì AA’ ⊥ (ABC) nên AB là hình chiếu của A’B trên (ABC).

Suy ra góc giữa đường thẳng A’B và mặt phẳng (ABC) bằng $\widehat{AB{A}^{\text{'}}}.$

Do A’B’BA là hình vuông nên đường chéo BA’ là phân giác của góc ABB’ nên $\widehat{AB{A}^{\text{'}}}=45°.$

Vậy góc giữa đường thẳng A’B và mặt phẳng (ABC) bằng 45°.

c) Do CC’ ⊥ (ABC) và BC, CM đều nằm trên (ABC).

Suy ra CC’ ⊥ BC, CC’ ⊥ CM.

Mà BC ∩ CM = C ∈ CC’.

Do đó $\widehat{BCM}$ là góc phẳng nhị diện của góc nhị diện [B, CC’, M].

Xét tam giác ABC đều có: CM là đường trung tuyến (do M là trung điểm của BC) nên đồng thời là đường phân giác của $\widehat{ACB}.$

Suy ra $\widehat{BCM}=\frac{\widehat{ACB}}{2}=\frac{60°}{2}=30°.$

Vậy số đo của góc nhị diện [B, CC, M] bằng 30°.

d) Do B’C’CB là hình vuông nên CC’ // BB’.

Mà BB’ ⊂ (ABB’A’) nên CC’ // (ABB’A’).

Khi đó d(CC’, (ABB’A’)) = d(C, (ABB’A’)).

Do AA’ ⊥ (ABC) và CM ⊂ (ABC) nên AA’ ⊥ CM.

Vì tam giác ABC đều có CM là đường trung tuyến nên đồng thời là đường cao của tam giác hay CM ⊥ AB.

Ta có: CM ⊥ AA’, CM ⊥ AB và AA’ ∩ AB = A trong (ABB’A’).

Suy ra CM ⊥ (ABB’A’).

Khi đó d(C, (ABB’A’)) = CM.

Do M là trung điểm của AB nên $BM=\frac{AB}{2}=\frac{a}{2}.$

Áp dụng định lí Pythagore vào tam giác CBM vuông tại M (do CM ⊥ AB) có:

BC² = BM² + CM²

Suy ra $CM=\sqrt{B{C}^2-B{M}^2}=\sqrt{a^2-{\left(\frac{a}{2}\right)}^2}=\frac{a\sqrt{3}}{2}.$

Do đó $d\left(C{C}^{\text{'}},\left(AB{B}^{\text{'}}{A}^{\text{'}}\right)\right)=d\left(C,\left(AB{B}^{\text{'}}{A}^{\text{'}}\right)\right)=CM=\frac{a\sqrt{3}}{2}.$

Vậy khoảng cách giữa đường thẳng CC’ và mặt phẳng (ABB’A’) bằng $\frac{a\sqrt{3}}{2}.$

e) Theo câu d ta có CM ⊥ (ABB’A’).

Mà A’M ⊂ (ABB’A’) nên CM ⊥ A’M.

Do CC’ ⊥ (ABC) và CM ⊂ (ABC) nên CC’ ⊥ CM.

Ta thấy: CM ⊥ A’M, CM ⊥ CC’.

Suy ra đoạn thẳng CM là đoạn vuông góc chung của hai đường thẳng CC’ và A’M.

Khi đó $d\left(C{C}^{\text{'}},A^{\text{'}}M\right)=CM=\frac{a\sqrt{3}}{2}.$

Vậy khoảng cách giữa hai đường thẳng CC’ và A’M bằng $\frac{a\sqrt{3}}{2}.$

g) ⦁ Diện tích tam giác ABC đều cạnh a có đường cao $CM=\frac{a\sqrt{3}}{2}$ là:

$S_{\Delta ABC}=\frac{1}{2}CM.AB=\frac{1}{2}.\frac{a\sqrt{3}}{2}.a=\frac{a^2\sqrt{3}}{4}.$

Thể tích của khối lăng trụ tam giác đều ABC.A’B’C’ có chiều cao AA’ = a và diện tích đáy $S_{\Delta ABC}=\frac{a^2\sqrt{3}}{4}$ là:

$V_{ABC.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}=S_{\Delta ABC}.A{A}^{\text{'}}=\frac{a^2\sqrt{3}}{4}.a=\frac{a^3\sqrt{3}}{4}.$

⦁ Vì A là hình chiếu của A’ trên (ABC) và (MBC) ≡ (ABC).

Suy ra A cũng là hình chiếu của A’ trên (MBC).

Nên ta có đoạn thẳng AA’ cũng là chiều cao của khối chóp A’.MBC.

Diện tích tam giác MBC vuông tại M là:

$S_{\Delta MBC}=\frac{1}{2}CM.MB=\frac{1}{2}.\frac{a\sqrt{3}}{2}.\frac{a}{2}=\frac{a^2\sqrt{3}}{8}.$

Thể tích của khối chóp tam giác A’.MBC có chiều cao AA’ = a và diện tích đáy $S_{\Delta MBC}=\frac{a^2\sqrt{3}}{8}$ là:

$V_{A^{\text{'}}.MBC}=\frac{1}{3}{S}_{\Delta MBC}.A{A}^{\text{'}}=\frac{1}{3}.\frac{a^2\sqrt{3}}{8}.a=\frac{a^3\sqrt{3}}{24}.$

Xem thêm các bài giải SGK Toán lớp 11 Cánh diều hay, chi tiết khác: