Bài 42 trang 113 SBT Toán 11: Cho hình hộp ABCD.A'B'C'D'. Gọi M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, CC', C'D', D'A', AA'. Chứng minh rằng:
a) Sáu điểm M, N, P, Q, R, S cùng thuộc một mặt phẳng.
b) Các đoạn thẳng MQ, NR, PS cắt nhau tại trung điểm của mỗi đoạn.
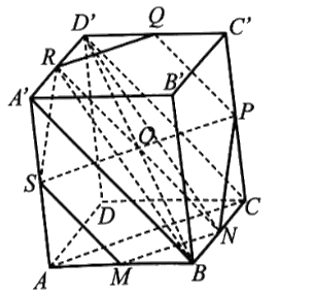
a) Ta có S và P lần lượt là trung điểm của AA' và CC'.
Suy ra .
Mà AA' = CC' và AA' // CC' (do ABCD.A'B'C'D' là hình hộp)
Nên AS = CP và AS // CP. Do đó, tứ giác ASPC là hình bình hành.
Suy ra AC // SP.
Mặt khác MN // AC (do MN là đường trung bình của tam giác ABC).
Khi đó, MN // SP.
Vậy M, N, P, S cùng thuộc một mặt phẳng.
Ta cũng chứng minh được PQ // CD', CD' // BA', BA' // MS nên PQ // MS.
Do đó Q ∈ (MNPS).
Tương tự ta có QR // MN nên R ∈ (MNPS).
Vậy sáu điểm M, N, P, Q, R, S cùng thuộc một mặt phẳng.
b) Gọi O là giao điểm của các đường chéo hình hộp ABCD.A'B'C'D'.
Khi đó, O là trung điểm của các đường chéo BD', B'D, AC', A'C.
Ta có tứ giác BND'R là hình bình hành, nên hai đường chéo BD', NR cắt nhau tại trung điểm O của mỗi đường.
Tương tự, ta chứng minh được QM, PS đều nhận O là trung điểm.
Vậy các đoạn thẳng MQ, NR, PS cắt nhau tại trung điểm của mỗi đoạn.
Xem thêm các bài giải SBT Toán lớp 11 Cánh diều hay, chi tiết khác:
Bài 2: Hai đường thẳng song song trong không gian
Bài 3: Đường thẳng và mặt phẳng song song
Bài 4: Hai mặt phẳng song song
Bài 5: Hình lăng trụ và hình hộp
Bài 6: Phép chiếu song song. Hình biểu diễn của một hình không gian