Câu hỏi:
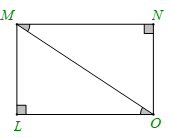
25/01/2024 68Cho hình chữ nhật ABCD, M là trung điểm của cạnh CD. Khẳng định sai là
A. \(\Delta ADM = \Delta BCM\);
B. AD = BM;
C. AD = BC;
D. \(\widehat {AMD} = \widehat {BMC}\).
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: B
ABCD là hình chữ nhật ⇒ AD = BC và \(\widehat {ADM} = \widehat {BCM} = 90^\circ \)
Xét tam giác ADM (vuông tại D) và tam giác BCM (vuông tại C) có:
AD = BC (chứng minh trên)
DM = CM (theo giả thiết)
⇒ \(\Delta ADM = \Delta BCM\) (hai cạnh góc vuông)
⇒ AD = BC; AM = BM (các cạnh tương ứng)
(hai góc tương ứng)
Vậy khẳng định B sai.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tam giác ABC vuông tại C và tam giác DEF vuông tại F, có \(\widehat B = \widehat E\). Cần thêm điều kiện gì để \(\Delta ABC = \Delta DEF\) theo trường hợp cạnh huyền - góc nhọn?
Câu 3:
Cho tam giác ABC vuông tại B và tam giác PMN vuông tại M có AC = PN, 
. Biết AB = 4 cm; AC = 5 cm. Chu vi tam giác PMN là 12 cm. Diện tích tam giác PMN là
Câu 4:
Cho tam giác ABC vuông tại B và tam giác MNP vuông tại N, có AB = MN. Cần thêm điều kiện gì để \(\Delta ABC = \Delta MNP\) theo trường hợp hai cạnh góc vuông?
Câu 6:
Cho tam giác ABC vuông tại A và tam giác POI vuông tại I có BC = OP, \(\widehat C = \widehat P\). Khẳng định đúng là
Câu 9:
Cho tam giác ABC vuông tại A và tam giác DEF vuông tại D, có AB = DE. Cần thêm điều kiện gì để \(\Delta ABC = \Delta DEF\) theo trường hợp cạnh góc vuông - góc nhọn kề?
Câu 10:
Cho hình vẽ dưới đây, biết AB vuông góc với BC, AD vuông góc với CD và cạnh AB = AD. Khẳng định sai là
Câu 12:
Cho tam giác ABC vuông tại C và tam giác MNO vuông tại O, có BC = NO. Cần thêm điều kiện gì để \(\Delta ABC = \Delta MNO\) theo trường hợp cạnh huyền – cạnh góc vuông?
Câu 14:
Cho tam giác ABC vuông tại A và tam giác PMN vuông tại P có AB = PM, AC = PN. Biết \(\widehat B = 60^\circ \). Số đo góc N là
