Cho hình chữ nhật ABCD có hai cạnh kề AB và BC bằng nhau. ABCD có phải là hình vuông hay không

Hoạt động 3 trang 118 Toán 8 Tập 1: a) Cho hình chữ nhật ABCD có hai cạnh kề AB và BC bằng nhau. ABCD có phải là hình vuông hay không?

b) Cho hình chữ nhật ABCD có hai đường chéo AC và BD vuông góc với nhau (Hình 69).

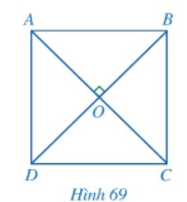
• Đường thẳng AC có phải là đường trung trực của thẳng BD hay không? đoạn

• ABCD có phải là hình vuông hay không?

c) Cho hình chữ nhật ABCD có AC là tia phân giác của góc DAB.

• Tam giác ABC có phải là tam giác vuông cân hay không?

• ABCD có phải là hình vuông hay không?

Trả lời

a) Do ABCD là hình chữ nhật nên $\widehat{A}=\widehat{B}=\widehat{C}=\widehat{D}=90°$ và AB = CD, AD = BC.

Mà AB = BC nên AB = BC = CD = DA.

Tứ giác ABCD có 4 góc vuông và 4 cạnh bằng nhau nên là hình vuông.

b) • Do ABCD là hình chữ nhật nên hai đường chéo AC và BD cắt nhau tại trung điểm O của mỗi đường.

Mà AC ⊥ BD

Do đó AC là đường trung trực của đoạn thẳng BD.

• Do ABCD là hình chữ nhật nên $\widehat{A}=\widehat{B}=\widehat{C}=\widehat{D}=90°$ và AB = CD; AD = BC.

Do AC là đường trung trực của đoạn thẳng BD nên AB = AD và CB = CD.

Do đó AB = BC = CD = DA.

Tứ giác ABCD có 4 góc vuông và 4 cạnh bằng nhau nên là hình vuông.

c)

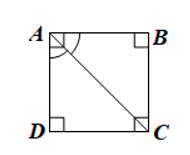
• Do ABCD là hình chữ nhật nên $\widehat{B}=90°$ và AD // BC

Từ AD // BC suy ra $\widehat{DAC}=\widehat{BCA}$ (so le trong).

Mặt khác, AC là tia phân giác của góc DAB nên $\widehat{DAC}=\widehat{BAC}$

Suy ra $\widehat{BAC}=\widehat{BCA}$ (vì cùng bằng $\widehat{DAC}$).

Tam giác ABC vuông tại B ($\widehat{B}=90°$) có $\widehat{BAC}=\widehat{BCA}$

Do đó ΔABC vuông cân tại B.

• Do ΔABC vuông cân tại B nên BA = BC.

Theo kết quả câu a, hình chữ nhật ABCD có hai cạnh kề BA và BC bằng nhau nên là hình vuông.

Xem thêm các bài giải SGK Toán lớp 8 Cánh Diều hay, chi tiết khác:

Bài 3: Hình thang cân

Bài 4: Hình bình hành