Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh a, tâm O. Gọi M và
54
23/04/2024
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh a, tâm O. Gọi M và N lần lượt là trung điểm của hai cạnh SA và BC, biết . Khi đó giá trị sin của góc giữa đường thẳng MN và mặt phẳng bằng
B.
C.
D.
Trả lời
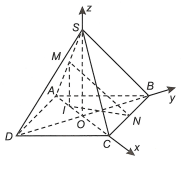
Gọi I hình chiếu của M lên , suy ra I là trung điểm của AO.
Khi đó .
Xét có .
Áp dụng định lý cosin ta có:
Xét vuông tại I nên
Mà .
Chọn hệ trục tọa độ Oxyz như hình vẽ:
Ta có ,
Khi đó .
Vecto pháp tuyến mặt phẳng : .
Suy ra .
Chọn B.

