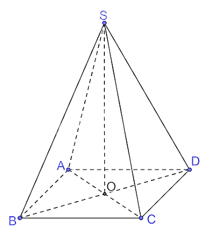
Cho hình chóp S.ABCD, đáy ABCD là một hình chữ nhật có tâm O, SO ^ (ABCD). Chứng minh rằng hai mặt phẳng (SAC) và (SBD) vuông góc với nhau khi và chỉ khi ABCD là một hình vuông.

Gọi O là giao điểm của AC và BD.

Vì SO ^ (ABCD) nên SO ^ AO và SO ^ BO mà (SAC) Ç (SBD) = SO, suy ra góc giữa hai mặt phẳng (SAC) và (SBD) bằng góc giữa hai đường thẳng AO và BO.

Mà (AO, BO) = $\widehat{AOB}$ .

+) Nếu (SAC) ^ (SBD) thì $\widehat{AOB}=90°$ , khi đó AC ^ BD mà ABCD là hình chữ nhật, suy ra ABCD là hình vuông.

+) Nếu ABCD là hình vuông thì AC ^ BD, suy ra $\widehat{AOB}=90°$  hay (SAC) ^ (SBD).