Cho hình chóp đều S.ABC, đáy có cạnh bằng a, cạnh bên bằng b.

a) Tính sin của góc tạo bởi cạnh bên và mặt đáy.

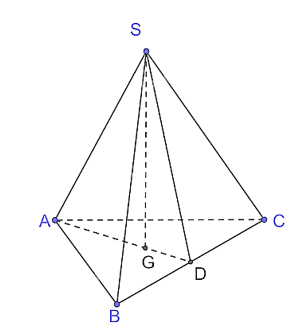
a) Gọi G là hình chiếu của S trên mặt phẳng (ABC).

Vì S.ABC đều nên G là tâm của tam giác ABC hay G là trọng tâm đồng thời G cũng là trực tâm của tam giác ABC.

Gọi a là góc tạo bởi cạnh bên SA và mặt phẳng đáy (ABC).

Vì SG ^ (ABC) nên GA là hình chiếu của SA trên mặt phẳng (ABC).

Khi đó góc giữa cạnh bên SA và mặt phẳng đáy (ABC) bằng góc giữa hai đường thẳng SA và AG. Mà (SA, AG) =  $\widehat{SAG}=\alpha$.

Kẻ AG cắt BC tại D, khi đó D là trung điểm của BC, AD ^ BC.

Xét tam giác ABC đều cạnh a, AD là đường cao nên $AD=\frac{a\sqrt{3}}{2}$ .

Suy ra $AG=\frac{2}{3}AD=\frac{2}{3}\cdot \frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{3}$

giác SGA vuông tại G, có $SG=\sqrt{S{A}^2-A{G}^2}=\sqrt{b^2-\frac{a^2}{3}}$ .

$\sin \widehat{SAG}=\frac{SG}{SA}=\frac{\sqrt{b^2-\frac{a^2}{3}}}{b}=\sqrt{\frac{3b^2-a^2}{3b^2}}=\sqrt{1-\frac{a^2}{3b^2}}$.

Vậy sin của góc tạo bởi cạnh bên và mặt đáy bằng $\sqrt{1-\frac{a^2}{3b^2}}$ .