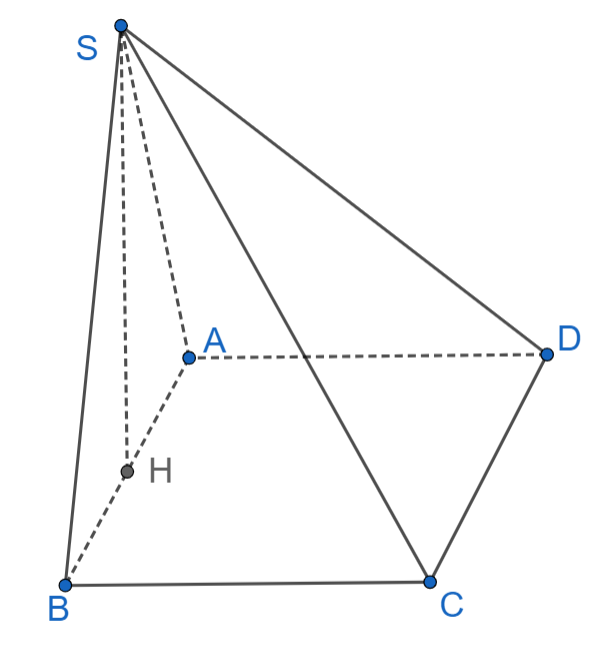
Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB = 2a, AD = a. Tam giác SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa mặt phẳng (SBC) và (ABCD) bằng 45°. Khi đó thể tích khối chóp S.ABCD là

A. $\frac{\sqrt{3}}{3}{a}^3$ .

B. $\frac{1}{3}{a}^3$ .

C. $2a^3$ .

D. $\frac{2a^3}{3}$ .

Đáp án đúng là: D

Gọi H là trung điểm của AB Þ SH ^ (ABCD).

Ta có: $\left\{\begin{array}{l}BC\perp AB\\ BC\perp SH\end{array}\right.\Rightarrow BC\perp \left(SAB\right)\Rightarrow BC\perp SB.$

$\Rightarrow \left(\left(SBC\right),\left(ABCD\right)\right)=\left(SB,AB\right)=\widehat{SBA}=45°.$

Þ ∆SHB là tam giác vuông cân tại H $\Rightarrow SH=HB=\frac{1}{2}AB=a.$

$\Rightarrow V_{S.ABCD}=\frac{1}{3}.SH.S_{ABCD}=\frac{1}{3}.a.2a.a=\frac{2a^3}{3}.$