Cho hình hộp đứng ABCD.A'B'C'D' có đáy ABCD là hình thoi cạnh 2a. Mặt phẳng (B'AC) tạo với đáy một góc 30°, khoảng cách từ B đến mặt phẳng (D'AC) bằng $\frac{a}{2}$ . Tính thể tích khối tứ diện ACB'D'.

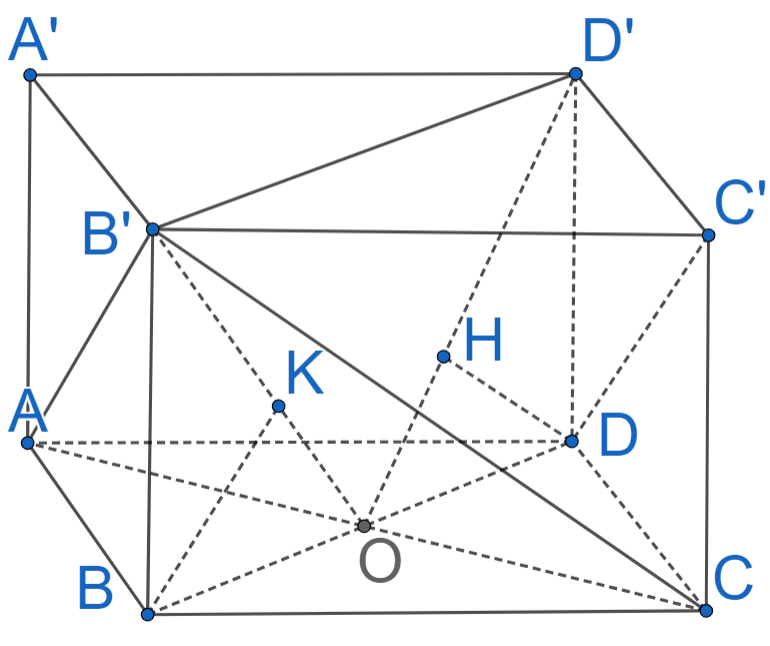
Gọi O = AC Ç BD. Ta có:

$\left\{\begin{array}{l}AC\perp BD\\ AC\perp BB\text{'}\end{array}\right.\Rightarrow AC\perp \left(BB\text{'}D\right)\Rightarrow AC\perp B\text{'}O.$

Khi đó: $BO\perp AC,B\text{'}O\perp AC,\left(ABCD\right)\cap \left(B\text{'}AC\right)=AC,$

$\Rightarrow \left(\left(B\text{'}AC\right),\left(ABCD\right)\right)=(BO,OB\text{'})=\widehat{B\text{'}OB}=30°.$

Dễ thấy $d\left(B,\left(D\text{'}AC\right)\right)=d\left(D,\left(D\text{'}AC\right)\right)=\frac{a}{2}$

$AC\perp (BB\text{'}D\text{'}D)\Rightarrow (D\text{'}AC)\perp (BB\text{'}D\text{'}D)$

$(D\text{'}AC)\cap (BB\text{'}D\text{'}D)=D\text{'}O.$

Từ D kẻ DH ^ D¢O (H Î DO), suy ra $d\left(D,\left(D\text{'}AC\right)\right)=DH=\frac{a}{2}.$

Xét ∆B¢BO: $\tan 30°=\frac{BB\text{'}}{BO}\Rightarrow OD=BO=\sqrt{3}BB\text{'}.$ 

Xét ∆D¢DO: $\frac{1}{H{D}^2}=\frac{1}{O{D}^2}+\frac{1}{D\text{'}{D}^2}\Rightarrow \frac{4}{a^2}=\frac{1}{3.B\text{'}{B}^2}+\frac{1}{D\text{'}{D}^2}$ $\Rightarrow DD\text{'}=\frac{a}{\sqrt{3}}\Rightarrow OB=a.$

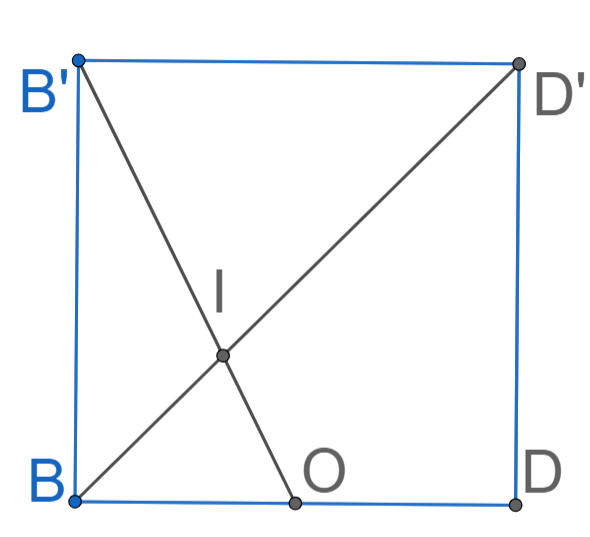
Gọi I = BD Ç B¢O, suy ra $\frac{BI}{D\text{'}I}=\frac{1}{2}.$

$\Rightarrow d\left(D\text{'},\left(B\text{'}AC\right)\right)=2d\left(B,\left(B\text{'}AC\right)\right)\Rightarrow V_{ACB\text{'}D\text{'}}=2V_{B\text{'}ABC}.$

Mà $OA=\sqrt{A{B}^2-O{B}^2}=\sqrt{4a^2-a^2}=a\sqrt{3}.$

$\Rightarrow S_{ABC}=2S_{ABO}=2.\frac{1}{2}.OB.OA=a^2\sqrt{3}.$

Suy ra $V_{B\text{'}.ABC}=\frac{1}{3}.BB\text{'}.S_{ABC}=\frac{1}{3}.\frac{a}{\sqrt{3}}.a^2\sqrt{3}=\frac{a^3}{3}.$

Vậy $V_{ACB\text{'}D\text{'}}=\frac{2a^3}{3}.$