Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau
37
01/11/2024
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau. Gọi H là hình chiếu của điểm O trên mặt phẳng (ABC). Chứng minh rằng:
a) BC ^ (OAH).
b) H là trực tâm của ∆ABC.
c) 1OH2=1OA2+1OB2+1OC2
Trả lời
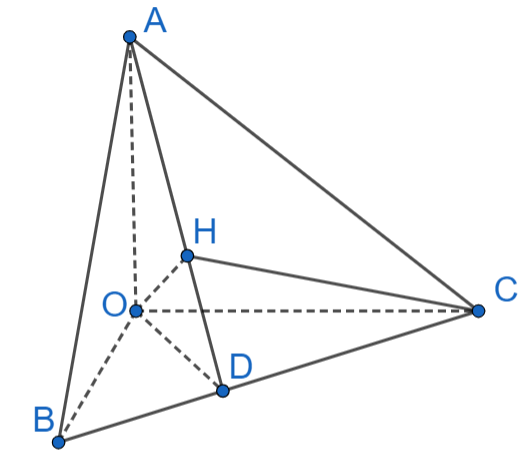
a) Ta có: {OA⊥OBOA⊥OC
⇒OA⊥(OBC)⇒OA⊥BC.(1)
OH⊥BC (OH⊥(ABC)).(2)
Từ (1) và (2) Þ BC ^ (OAH).
b) Từ a) Þ BC ^ AH. (*)
Ta dễ dàng chứng minh được OC ^ (OAB) Þ OC ^ AB. (3)
Lại có: OH ^ AB (do OH ^ (ABC)) Þ OH ^ AB. (4)
Từ (3) và (4) Þ AB ^ (OHC) hay AB ^ HC. (**)
Từ (*) và (**) Þ H là trực tâm của tam giác ABC.
c) Dễ thấy OD, OH là các đường cao của tam giác OBC và OAD.
Áp dụng hệ thức lượng trong tam giác vuông, ta có:
{1OD2=1OB2+1OC21OH2=1OA2+1OD2
Do đó 1OH2=1OA2+1OB2+1OC2.

