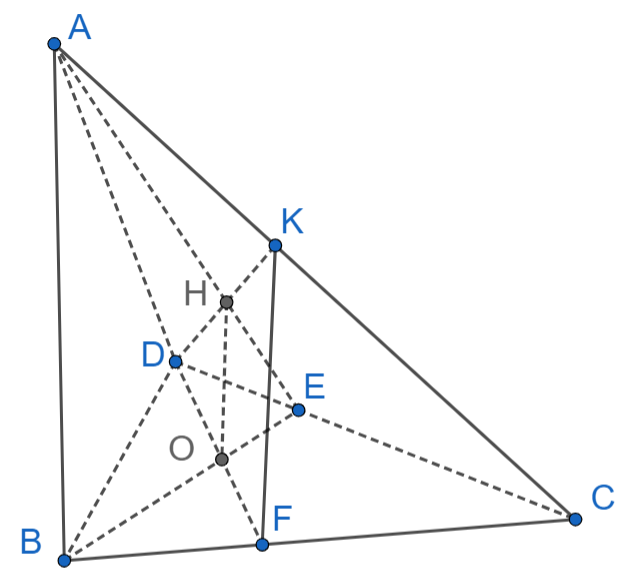
Cho tứ diện ABCD có hai mặt phẳng (ABC) và (ABD) cùng vuông góc với (DBC). Vẽ các đường cao BE, DF của tam giác BCD, đường cao DK của tam giác ACD.

a) Chứng minh hai mặt phẳng (ABE) và (DFK) cùng vuông góc với (ADC).

b) Gọi O và H là trực tâm ∆BCD và ∆ACD. Chứng minh OH vuông góc với (ADC).

a) Từ giả thiết suy ra AB ^ (BDC) Þ AB ^ DC.

Lại có: BE ^ DC.

Þ DC ^ (ABE) hay (ADC) ^ (ABE).   (1)

Ta có: $\left\{\begin{array}{l}DF\perp BC\\ DF\perp AB\end{array}\right.\Rightarrow DF\perp \left(ABC\right)\Rightarrow DF\perp AC.$

Mà DK ^ AC.

Do đó AC ^ (DFK) hay (ADC) ^ (DFK).             (2)

b) Dễ thấy O, H lần lượt là các giao điểm của DF và BE, AE và DK.

Þ (ABE) Ç (DFK) = OH.      (3)

Từ (1), (2) và (3) Þ OH ^ (ADC).