Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = 2a, BC = a, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi E là trung điểm của CD. Tính theo a khoảng cách giữa hai đường thẳng BE và SC.

A. $\frac{a\sqrt{30}}{10}$ .

B. $\frac{a\sqrt{15}}{5}$.

C. $\frac{a\sqrt{3}}{2}$

D. a.

Đáp án đúng là: A

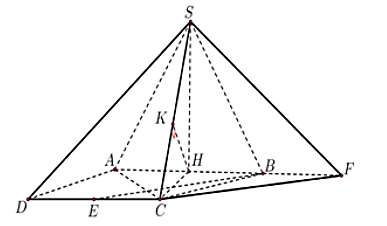
Gọi H là trung điểm AB.

Do $\left\{\begin{array}{l}\left(SAB\right)\cap \left(ABCD\right)=AB\\ \left(SAB\right)\perp \left(ABCD\right)\\ SH\perp AB,SH\subset \left(SAB\right)\end{array}\right.\Rightarrow SH\perp \left(ABCD\right).$

F đối xứng với H qua B Þ BECF là hình bình hành.

BE // CF Ì (SCF) Þd(BE, (SCF)) = d(B, (SCF)) = $\frac{1}{2}$ d(H, (SCF)).

HBCE là hình vuông cạnh a Þ $CH=BE=CF=a\sqrt{2}.$

Dễ thấy $C{H}^2+C{F}^2=4a^2=H{F}^2$   Þ ∆HCF vuông cân tại C.

Khi này $\left\{\begin{array}{l}CF\perp HC\\ CF\perp SH\end{array}\right.\Rightarrow CF\perp \left(SHC\right)\Rightarrow \left(SCF\right)\perp \left(SHC\right).$

Mà (SCF) Ç (SHC) = SC. Trong (SHC) kẻ HK ^ SC Þ HK ^ (SCF).

Suy ra d(H, (SCF)) = HK Þ d(BE, SC) = $\frac{1}{2}$  HK.

Áp dụng hệ thức lượng trong ∆SHC vuông tại H, đường cao HK

Þ $HK=\frac{a\sqrt{30}}{5}$

Vậy $d\left(BE,SC\right)=\frac{1}{2}HK=\frac{a\sqrt{30}}{10}$