Cho hình chóp S.ABC có SA ⊥ (ABC), AB = AC = a, góc BAC = 120°, SA= a/(2 căn 3)

Luyện tập 4 trang 48 Toán 11 Tập 2: Cho hình chóp S.ABC có SA ⊥ (ABC), AB = AC = a, $\widehat{BAC}=120°,SA=\frac{a}{2\sqrt{3}}$. Gọi M là trung điểm của BC.

a) Chứng minh rằng $\widehat{SMA}$ là một góc phẳng của góc nhị diện [S, BC, A].

b) Tính số đo của góc nhị diện [S, BC, A].

Trả lời

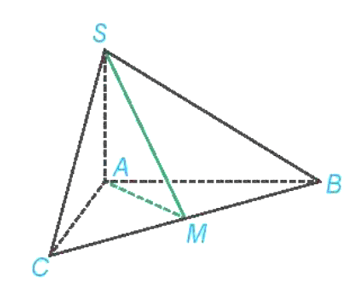
a) Xét tam giác ABC có AB = AC nên tam giác ABC cân tại A mà AM là trung tuyến nên AM là đường cao hay AM ⊥ BC.

Vì SA ⊥ (ABC) nên SA ⊥ BC mà AM ⊥ BC, suy ra BC ⊥ (SAM), do đó BC ⊥ SM.

Vì AM ⊥ BC và BC ⊥ SM nên $\widehat{SMA}$là một góc phẳng của góc nhị diện [S, BC, A].

b) Áp dụng định lí Côsin cho tam giác ABC, có:

$B{C}^2=A{B}^2+A{C}^2–2\cdot AB\cdot AC\cdot cos\widehat{BAC}$ $=a^2+a^2–2\cdot a\cdot a\cdot cos120°$ $=2a^2+2a^2\cdot \frac{1}{2}=3a^2$ $\Rightarrow BC=a\sqrt{3}$.

Vì M là trung điểm của BC nên $BM=MC=\frac{a\sqrt{3}}{2}$.

Xét tam giác AMB vuông tại M, có $AM=\sqrt{A{B}^2-B{M}^2}=\sqrt{a^2-\frac{3a^2}{4}}=\frac{a}{2}$

Vì SA ⊥ (ABC) nên SA ⊥ AM.

Xét tam giác SAM vuông tại A, có: $\tan \widehat{SMA}=\frac{SA}{AM}=\frac{\frac{a}{2\sqrt{3}}}{\frac{a}{2}}=\frac{1}{\sqrt{3}}$ $\Rightarrow \widehat{SMA}=30°$.

Vậy số đo của góc nhị diện [S, BC, A] bằng 30°.

Xem thêm các bài giải SGK Toán lớp 11 Kết nối tri thức hay, chi tiết khác:

Bài 23: Đường thẳng vuông góc với mặt phẳng

Bài 24: Phép chiếu vuông góc. Góc giữa đường thẳng và mặt phẳng

Bài 25: Hai mặt phẳng vuông góc

Bài 26: Khoảng cách

Bài 27: Thể tích

Bài tập cuối chương 7