Câu hỏi:
03/04/2024 50
Cho hình chóp SABC có và . Hình chóp SABC có bao nhiêu mặt là tam giác vuông?
A. 4
B. 3
C. 2
D. 1
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
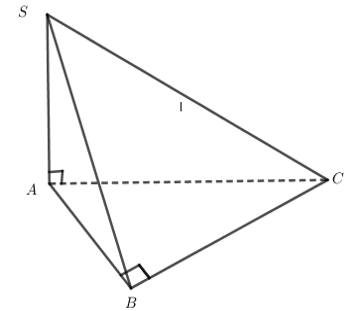
Ta có vuông tại A ( Do )
vuông tại A ( Do )
vuông tại B ( Do ).
Lại có mà suy ra nên vuông tại B.
Vậy Hình chóp SABC có 4 mặt là tam giác vuông.

Ta có vuông tại A ( Do )
vuông tại A ( Do )
vuông tại B ( Do ).
Lại có mà suy ra nên vuông tại B.
Vậy Hình chóp SABC có 4 mặt là tam giác vuông.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hình chóp S.ABC có ; tam giác ABC đều cạnh a và SA=a. Tìm góc giữa SC và mặt phẳng .
Câu 3:
Cho hai đường thẳng a,b phân biệt và mặt phẳng P . Mệnh đề nào sau đây sai?
Câu 5:
Cho hình vuông ABCD có cạnh bằng a Người ta dựng hình vuông có cạnh bằng đường chéo của hình vuông ABCD; dựng hình vuông có cạnh bằng đường chéo của hình vuông và cứ tiếp tục như vậy. Giả sử cách dựng trên có thể tiến ra vô hạn. Nếu tổng diện tích S của tất cả các hình vuông bằng 8 thì a bằng:
Cho hình vuông ABCD có cạnh bằng a Người ta dựng hình vuông có cạnh bằng đường chéo của hình vuông ABCD; dựng hình vuông có cạnh bằng đường chéo của hình vuông và cứ tiếp tục như vậy. Giả sử cách dựng trên có thể tiến ra vô hạn. Nếu tổng diện tích S của tất cả các hình vuông bằng 8 thì a bằng:
Câu 6:
Cho tứ diện đều ABCD cạnh a Gọi M là trung điểm của BC . Tính cosin của góc giữa hai đường thẳng AB và DM
Câu 11:
Cho tứ diện ABCD có AC= 6a, BD=8a. Gọi M,N lần lượt là trung điểm của AD, BC Biết Tính độ dài đoạn thẳng MN
Cho tứ diện ABCD có AC= 6a, BD=8a. Gọi M,N lần lượt là trung điểm của AD, BC Biết Tính độ dài đoạn thẳng MN
Câu 12:
Cho hình chóp SABCD có đáy là hình vuông ABCD, và . Gọi E, F lần lượt là trung điểm của BC, SC. Góc giữa EF và mặt phẳng (SAD) bằng
Cho hình chóp SABCD có đáy là hình vuông ABCD, và . Gọi E, F lần lượt là trung điểm của BC, SC. Góc giữa EF và mặt phẳng (SAD) bằng
Câu 15:
Cho hình chóp SABC có Gọi I là hình chiếu vuông góc của S lên mặt phẳng (ABC) Chọn khẳng định đúng trong các khẳng định sau.
Cho hình chóp SABC có Gọi I là hình chiếu vuông góc của S lên mặt phẳng (ABC) Chọn khẳng định đúng trong các khẳng định sau.


