Bài 16 trang 74 SBT Toán 8 Tập 1: Cho hình bình hành ABCD. Trên đường chéo BD lấy hai điểm M và N sao cho BM = DN.
a) Chứng minh tứ giác AMCN là hình bình hành.
b) Xác định vị trí của điểm M để tia AM cắt BC tại trung điểm của BC.
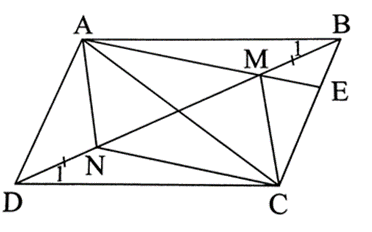
a) ABCD là hình bình hành nên AB = CD và AB // CD.
Xét ∆ABM và ∆CDN có:
AB = CD (chứng minh trên);
(hai góc so le trong do AB // CD);
BM = DN (giả thiết).
Do đó ∆ABM= ∆CDN (c.g.c).
Suy ra AM = CN (hai cạnh tương ứng)
Xét ∆AND và ∆CMB có:
AD = BC (do ABCD là hình bình hành);
(hai góc so le trong do AD // BC);
DN = BM (giả thiết).
Do đó ∆AND = ∆CMB (c.g.c).
Suy ra AN = CM (hai cạnh tương ứng).
Xét tứ giác AMCN có: AM = CN (chứng minh trên) và AN = CM (chứng minh trên)
Do đó, tứ giác AMCN là hình bình hành.
b) Gọi E là giao điểm của tia AM và BC.
Xét ∆BNC có ME // CN và E là trung điểm của BC (giả thiết)
Theo bài 5, trang 63, SBT Toán 8 Tập Một, ta có: M là trung điểm của BN
Do đó BM = MN, mà BM = DN (giả thiết) nên BM = MN = ND
Suy ra .
Xem thêm các bài giải sách bài tập Toán 8 Chân trời sáng tạo hay, chi tiết khác:
Bài 4: Hình bình hành – Hình thoi
Bài 5: Hình chữ nhật – Hình vuông
Bài tập cuối chương 3 trang 72
Bài 1: Thu thập và phân loại dữ liệu