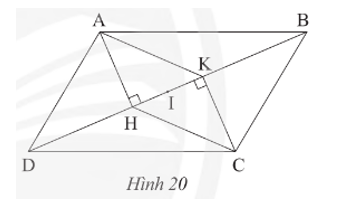
Cho hình bình hành ABCD, kẻ AH vuông góc với BD tại H và CK vuông góc với BD tại K (Hình 20).

a) Chứng minh tứ giác AHCK là hình bình hành.

a) Do ABCD là hình bình hành nên AD // BC và AD = BC.

Do AD // BC nên $\widehat{ADB}=\widehat{CBD}$ (so le trong)

Xét DADH và DCBK có:

$\widehat{AHD}=\widehat{CKB}=90°$;

AD = BC (chứng minh trên);

$\widehat{ADH}=\widehat{CBK}$ (do $\widehat{ADB}=\widehat{CBD}$).

Do đó DADH = DCBK (cạnh huyền – góc nhọn).

Suy ra AH = CK (hai cạnh tương ứng).

Ta có AH ⊥ DB và CK ⊥ DB nên AH // CK.

Tứ giác AHCK có AH // CK và AH = CK nên AHCK là hình bình hành (dấu hiệu nhận biết).