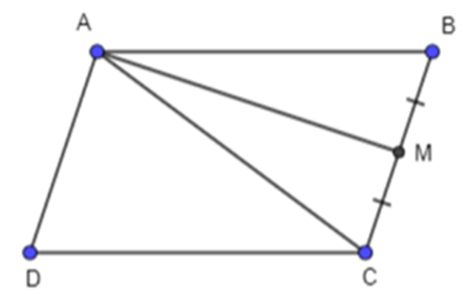
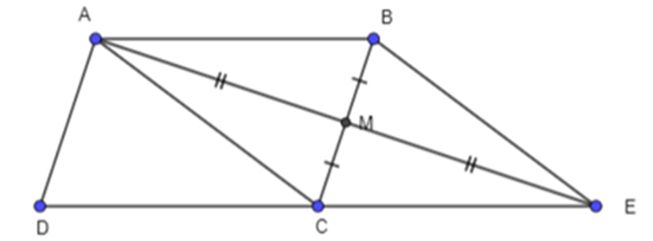
Cho hình bình hành ABCD. Gọi M là trung điểm cạnh BC. Hãy biểu thị \[\overrightarrow {{\rm{AM}}} \] theo \[\overrightarrow {{\rm{AB}}} \] và \[\overrightarrow {{\rm{AD}}} {\rm{.}}\]
Ta có hình vẽ sau:
Gọi E là điểm đối xứng với A qua M. Khi đó ABEC là hình bình hành
Ta có: \[\overrightarrow {{\rm{AB}}} {\rm{ + }}\overrightarrow {{\rm{AC}}} {\rm{ = }}\overrightarrow {{\rm{AE}}} \] (quy tắc hình bình hành)
Mà \[\overrightarrow {{\rm{AE}}} {\rm{ = 2}}\overrightarrow {{\rm{AM}}} \]
\[ \Rightarrow \overrightarrow {{\rm{AM}}} {\rm{ = }}\frac{{\overrightarrow {{\rm{AB}}} {\rm{ + }}\overrightarrow {{\rm{AC}}} }}{{\rm{2}}}\]
Ta lại có: \[\overrightarrow {{\rm{AC}}} {\rm{ = }}\overrightarrow {{\rm{AB}}} {\rm{ + }}\overrightarrow {{\rm{AD}}} \] (quy tắc hình bình hành)
\[ \Rightarrow \overrightarrow {{\rm{AM}}} {\rm{ = }}\frac{{\overrightarrow {{\rm{AB}}} {\rm{ + }}\overrightarrow {{\rm{AB}}} {\rm{ + }}\overrightarrow {{\rm{AD}}} }}{{\rm{2}}}{\rm{ = }}\frac{{{\rm{2}}\overrightarrow {{\rm{AB}}} {\rm{ + }}\overrightarrow {{\rm{AD}}} }}{{\rm{2}}}{\rm{ = }}\overrightarrow {{\rm{AB}}} {\rm{ + }}\frac{{\rm{1}}}{{\rm{2}}}\overrightarrow {{\rm{AD}}} {\rm{.}}\]
Vậy \[\overrightarrow {{\rm{AM}}} {\rm{ = }}\overrightarrow {{\rm{AB}}} {\rm{ + }}\frac{{\rm{1}}}{{\rm{2}}}\overrightarrow {{\rm{AD}}} {\rm{.}}\]