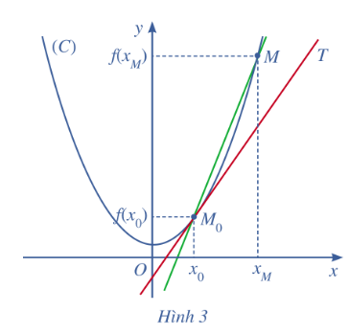
Cho hàm số y = f(x) có đồ thị (C), một điểm M₀ cố định thuộc (C) có hoành độ x₀. Với mỗi điểm M thuộc (C) khác M₀, kí hiệu x_M là hoành độ của điểm M và k_M là hệ số góc của cát tuyến M₀M. Giả sử tồn tại giới hạn hữu hạn $k_0=\underset{x_M\to x_0}{\lim }{k}_M.$ Khi đó, ta coi đường thẳng M₀T đi qua M₀ và có hệ số góc k₀ là vị trí giới hạn của cát tuyến M₀M khi điểm M di chuyển dọc theo (C) dần tới M₀.

Đường thẳng M₀T được gọi là tiếp tuyến của (C) tại điểm M₀, còn M₀ được gọi là tiếp điểm (Hình 3).

a) Xác định hệ số góc k₀ của tiếp tuyến M₀T theo x₀.

a) Từ M₀(x₀; y₀) và M(x_M; y_M) ta có $\overrightarrow{M_{0}M}=\left(x_M-x_0;y_M-y_0\right)$

Đường cát tuyến M₀M nhận $\overrightarrow{M_{0}M}=\left(x_M-x_0;y_M-y_0\right)$ làm vectơ chỉ phương nên có hệ số góc là $k_M=\frac{y_M-y_0}{x_M-x_0}=\frac{f\left(x_M\right)-f\left(x_0\right)}{x_M-x_0}$

Khi đó $k_0=\underset{x_M\to x_0}{\lim }{k}_M=\underset{x_M\to x_0}{\lim }\frac{f\left(x_M\right)-f\left(x_0\right)}{x_M-x_0}=f^{\text{'}}\left(x_0\right).$

Vậy k₀ = f’(x₀).